Xác định giá trị m để ba điểm A(3;1) ; B(2;-5) ; C(-1;m+2) tạo thành 1 tam giác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Bạn bổ sung đề đi bạn
b: thay x=-3 và y=0 vào (d), ta được:
\(-3\left(2m+1\right)-m+3=0\)
=>-6m-3-m+3=0
=>-7m=0
=>m=0
d: y=(2m+1)x-m+3
=2mx+x-m+3
=m(2x-1)+x+3
Tọa độ điểm cố định mà (1) luôn đi qua là:
\(\left\{{}\begin{matrix}2x-1=0\\y=x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=3+\dfrac{1}{2}=\dfrac{7}{2}\end{matrix}\right.\)

Hàm số đi qua điểm A(1;2) nên tọa độ của A(1;2) sẽ thỏa mãn phương trình hàm số:
2 = (m - 3).1 ⇔ m - 3 = 2 ⇔ m = 5
Ta có hàm số y = 2x

1: Để hai đường song song thì m+3=2
hay m=-1
3: Tọa độ của điểm A là:
\(\left\{{}\begin{matrix}y_A=0\\2x+4=0\end{matrix}\right.\Leftrightarrow A\left(-2;0\right)\)
Tọa độ điểm B là:
\(\left\{{}\begin{matrix}y_B=0\\-x+4=0\end{matrix}\right.\Leftrightarrow B\left(4;0\right)\)

b: Thay x=0 và y=-3 vào y=(m-1)x+m+1, ta được:
m+1=-3
hay m=-4
c: Thay x=1 và y=2 vào (d), ta được:
m-1+m+1=2
=>2m=2
hay m=1
d: Để hai đường trùng nhau thì \(\left\{{}\begin{matrix}m-1=2\\m+1=-1\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
e: Để hai đường song song thì m-1=-2
hay m=-1

Điều kiện: m – 3 ≠ 0 ⇔ m ≠ 3
Đồ thị của hàm số y = (m – 3)x đi qua điểm A(1; 2) nên tọa độ điểm A nghiệm đúng phương trình hàm số.
Ta có: 2 = (m – 3).1 ⇔ 2 = m – 3 ⇔ m = 5
Giá trị m = 5 thỏa mãn điều kiện bài toán.
Vậy với m = 5 thì đồ thị hàm sô y = (m – 3)x đi qua điểm A(1; 2).

Tập xác định ![]() .
.
Tính ![]() .
.
Để hàm số có ![]() điểm cực trị khi
điểm cực trị khi
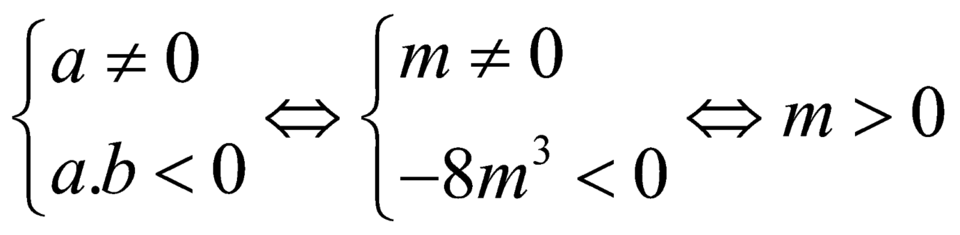 .
.
Chọn B
 help me pls
help me pls
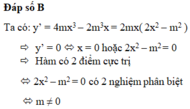
Gọi pt đường thẳng AB có dạng \(y=ax+b\)
\(\Rightarrow\left\{{}\begin{matrix}3a+b=1\\2a+b=-5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=6\\b=-17\end{matrix}\right.\) \(\Rightarrow y=6x-17\)
Để A;B;C tạo thành tam giác \(\Leftrightarrow A;B;C\) ko thẳng hàng
\(\Rightarrow C\notin AB\)
\(\Rightarrow6.\left(-1\right)-17\ne m+2\)
\(\Leftrightarrow m\ne-25\)