Tìm bội chung nhỏ nhất của
a] 35 và 40
b] 78 và 10
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
1
HQ
Hà Quang Minh
Giáo viên
2 tháng 10 2023
a) Do 5 và 7 là hai số nguyên tố cùng nhau nên:
BCNN(5, 7) = 5.7 = 35 => BC(5, 7) = B(35) = {0; 35; 70; 105; 140; 175; 210; ...}
Vậy bội chung nhỏ hơn 200 của 5 và 7 là 0; 35; 70; 105; 140; 175.
b) Ta có: 3 = 3; 4 = 22; 10 = 2.5
Không có thừa số nguyên tố chung ; thừa số nguyên tố riêng là 2,3,5. Số mũ lớn nhất của 2;3;5 lần lượt là 2;1;1 nên BCNN(3, 4, 10) = 22.3.5 = 60
=> BC(3, 4, 10) = B(60) = {0; 60; 120; 180; 240; ...}
Vậy bội chung nhỏ hơn 200 của 3, 4 và 10 là 0; 60; 120; 180.
LL
2 tháng 7 2023
`8)`
`a)` `->` ta được BCNN `(7;9;6)=126`
`->` từ đó ta có được BC `(7;9;6)={0;126;252;...}`
`b)` `->` ta được BCNN `(8;12;15)=120`
`->` từ đó ta được BC `(8;12;15)={0;120;240;...}`
`9)`
`a)->` BCNN `(15;18)=90`
`e)->` BCNN`(33;44;55)=660`
`b)->` BCNN`(8;18;30)=360`
`f)->` BCNN`(10;12)=60`
`c)->` BCNN `(4;14;26)=364`
`g)->` BCNN `(24;10)=210`
`d)->` BCNN `(6;8;10)=120`
2 tháng 7 2023
2 bài này khá dài khi giải ra nên mik chỉ giảng cách tính thôi:
Bước 1: Phân tích từng số ra tích các thừa số nguyên tố.
Bước 2: Tìm BCNN bằng cách nhân các thừa số nguyên tố với nhau với số mũ lớn nhất (nếu có chung)
TN
23 tháng 12 2021
a) Vì nên (n + 1) ∈ Ư(6) = {1; 2; 3; 6}
Ta có bảng sau:
n + 1 | 1 | 2 | 3 | 6 |
n | 0 | 1 | 2 | 5 |
Vì n là số tự nhiên nên n ∈ {0; 1; 2; 5}
Vậy n ∈ {0; 1; 2; 5}.
b) Gọi x = 23.3a và y = 2b.35
Ta có tích của hai số là tích của ƯCLN và BCNN của hai số đó.
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là và bội chung nhỏ nhất của hai số là 23.36.
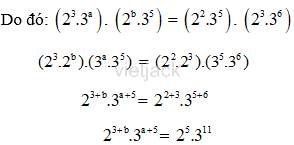
Vì thế 3 + b = 5. Suy ra b = 5 – 3 = 2
a + 5 = 11. Suy ra a = 11 – 5 = 6
Vậy a = 6; b = 2.
DN
11 tháng 11 2022
Gọi x = 23.3a và y = 2b.35
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là 22.35 và bội chung nhỏ nhất của hai số là 23.36
Ta được x.y=
Mà xy =
Ta được 5=3+b và 11=a+5
Vậy b=2 và a=6
1 tháng 1 2022
a: \(n+1\in\left\{1;2;3;6\right\}\)
hay \(n\in\left\{0;1;2;5\right\}\)
a , 280
b , 390
HT