A,ab= 125cm, cd=625cm
B, ef=45cm, e'f' =13,5dm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, \(\frac{AB}{CD}=\frac{120}{480}=\frac{1}{4}\)
b, 10,5 dm = 105 cm
\(\frac{EF}{E'F'}=\frac{45}{105}=\frac{3}{7}\)
c, \(\frac{MN}{M'N'}=\frac{555}{999}=\frac{5}{9}\)
d, 303,03m = 30303cm
\(\frac{PQ}{P'Q'}=\frac{10101}{30303}=\frac{1}{3}\)
Chúc bạn học tốt!!

a\()\)
Sơ đồ tạo ảnh
AB → A’B’
d d’
Công thức thấu kính: 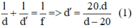
Gọi khoảng cách từ vật tới ảnh là L ⇒ |d’ + d| = L.
Vật thật ⇒ d > 0
L = 125cm
∗ Trường hợp 1: A’B’ là ảnh thật → d’ > 0
→ L = d’ + d =125cm (2)
Từ (1) và (2) ta có:
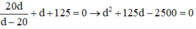
Giải phương trình lấy nghiệm d1 > 0 ta được: d1 = 17,54 cm
∗ Trường hợp 2
d’ + d = - 125cm (trường hợp này thì ảnh A’B’ là ảnh ảo) (3)
Từ (1) và (3) ta có:
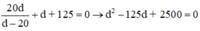
Giải phương trình lấy nghiệm d > 0 ta được: d = 25cm hoặc d = 100cm
a\()\)
Sơ đồ tạo ảnh
AB → A’B’
d d’
Công thức thấu kính: 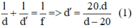
Gọi khoảng cách từ vật tới ảnh là L ⇒ |d’ + d| = L.
Vật thật ⇒ d > 0
L = 125cm
∗ Trường hợp 1: A’B’ là ảnh thật → d’ > 0
→ L = d’ + d =125cm (2)
Từ (1) và (2) ta có:
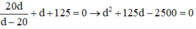
Giải phương trình lấy nghiệm d1 > 0 ta được: d1 = 17,54 cm
∗ Trường hợp 2
d’ + d = - 125cm (trường hợp này thì ảnh A’B’ là ảnh ảo) (3)
Từ (1) và (3) ta có:
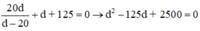
Giải phương trình lấy nghiệm d > 0 ta được: d = 25cm hoặc d = 100cm

Công thức tính thấu kính: \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow d'=\dfrac{12d}{d-12}\left(1\right)\)
Gọi khoảng cách từ vật tới ảnh là \(L\): \(\Rightarrow\) \(\left|d+d'\right|=L\)
Vật là vật thật \(\Rightarrow d>0\)
a) Ta có: \(L=125\left(cm\right)\)
TH1: A'B' là ảnh thật ⇒ \(d'>0\)
\(\Rightarrow L=d'+d=125\left(cm\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\dfrac{12d}{d-12}+d-125=0\Rightarrow d^2-125d+1500=0\)
Giải phương trình lấy nghiệm \(d_1>0\) ta được: \(d_1=111,55cm\) hoặc \(d_1=13,44cm\)
TH2: A'B' là ảnh ảo
\(d'+d=-125cm\left(3\right)\)
Từ (1) và (3) \(\Rightarrow\dfrac{12d}{d-12}+d+125=0\Rightarrow d^2+125d-1500=0\)
Giải phương trình lấy nghiệm \(d>0\) ta được: \(d_1=11\left(cm\right)\)
b) Ta có: \(L=45\left(cm\right)\)
TH1: A'B' là ảnh thật ⇒ \(d>0\)
\(\Rightarrow L=d'+d=45\left(cm\right)\left(4\right)\)
Từ (1) và (4) \(\Rightarrow\dfrac{12d}{d-12}+d-45=0\Leftrightarrow d^2-45d+540=0\)
Phương trình vô nghiệm
TH2: A'B' là ảnh ảo
\(d'+d=-45\left(cm\right)\left(5\right)\)
Từ (1) và (5) \(\Rightarrow\dfrac{12d}{d-12}+d+45\Leftrightarrow d^2+45d-540=0\)
Giải phương trình lấy nghiệm \(d_2>0\) ta được: \(d_2=9,85\left(cm\right)\)

theo ta-let ta có:
AI trên DK = IB trên KC (=MI trên MK)
AI trên KC = IB trên DK (=IN trên NK)
nhân thẳng hàng dược
AI^ 2 trên DK. KC = IB^2 trên DK .KC
suy ra AI= IB
mà AI trên DK = IB trên KC nên DK= kC
DPCM

a: Xét hình thang ABCD có
E là trung điểm của AD
F là trung điểm của BC
Do đó: EF là đường trung bình của hình thang ABCD
Suy ra: \(EF=\dfrac{AB+CD}{2}\)
hay CD=12cm
a. Ta có:
\(\frac{AB}{CD}=\frac{125}{625}=\frac{1}{5}\)
b. Đổi: E’F’ = 13,5dm = 135 cm
Ta có:
\(\frac{EF}{E'F'}=\frac{45}{135}=\frac{1}{3}\)