Không sử dụng thước đo góc, tính số đo 𝑥 trong các hình vẽ sau:

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Các góc có trong hình vẽ là : \(\widehat{ABC} ; \widehat{BAC} ; \widehat{CAB} ; \widehat{BDA} ; \widehat{DAB} ; \widehat{ABD} ; \widehat{DBC} ; \widehat{DAC}\)
Những góc có số đo bằng 60 độ là : \(\widehat{ABC} ; \widehat{BAC} ; \widehat{CAB}\)
b, Điểm D có nằm trong góc ABC. Điểm C không nằm trong góc ADB.
c, Số đo góc ABD là: 40o.

Độ bền sản phẩm cao, vật liệu cao cấp. Vạch chia và thang đo rõ nét, có vít vặn lớn để cố định vị trí cho kết quả đo nhanh và chính xác.
Thước đo ở hình 5.4 khác với thước đo góc thường sử dụng trên giấy là đây là thước đo góc vạn năng.

Sau khi đo độ dài các cạnh và các góc, ta thấy \(ABCD\), \(EFGH\) là các hình thang cân.

Góc đỉnh M cạnh MP, MN có số đo là 60°.
Góc đỉnh D cạnh DC, DE có số đo là 120°.
Góc đỉnh O cạnh OA, OB có số đo là 90°.
Góc đỉnh H cạnh HG, HK có số đo là 180°.

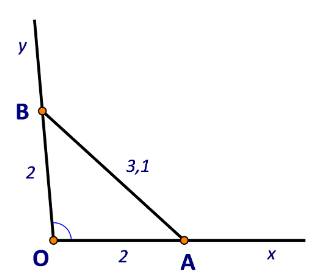
Áp dụng định lí cosin trong tam giác OAB, ta có:
\(\begin{array}{l}\cos O = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}} = \frac{{{2^2} + {2^2} - 3,{1^2}}}{{2.2.2}} \approx - 0,2\\ \Rightarrow \widehat {xOy} \approx {102^o}\end{array}\)
Bạn chỉ cần vận dụng cái tổng 3 góc của 1 tam giác là dc mà
Còn cái x thì là gộp thành nhân 2x hoặc 3x
Sau đó lấy 180 : cho là ra
Hình 1 :
Vì tông 3 góc trong 1 tam giác luôn bằng 180o nên \(\widehat{B}+\widehat{C}+x=180^o\)
\(\Rightarrow55^o+35^o+x=180^o\)\(\Rightarrow90^o+x=180^o\Rightarrow x=180^o-90^o=90^o\)
Tương tự với hình 2 , ta tính được :
Hình 2 : \(x=110^o\)
Hình 3 :
Vì tổng 3 góc trong 1 tam giác luôn bằng 180o nên : \(\widehat{N}+x+x=180^o\)
\(\Rightarrow50^o+2x=180^o\Rightarrow2x=180^o-50^o=130^o\Rightarrow x=65^o\)
Hình 5 :
Vì AB ⊥ AC => \(\widehat{B}=90^o\)mà tổng 3 góc trong 1 tam giác luôn bằng 180o nên :
\(\widehat{A}+60^o+x=180^o\)\(\Rightarrow60^o+x=120^o\)\(\Rightarrow x=60^o\)
Hình 6 :
Vì IH ⊥ HG => \(\widehat{H}=90^o\)mà tổng 3 góc trong 1 tam giác luôn bằng 180o nên :
\(90^o+x+x=180^o\Rightarrow2x=90^o\Rightarrow x=45^o\)
Hình 7 :
Vì KJ ⊥ JL => \(\widehat{J}=90^o\)mà tổng 3 góc trong 1 tam giác luôn bằng 180o nên :
\(90^o+2x+x=180^o\)\(\Rightarrow3x=90^o\Rightarrow x=30^o\)