giải phương trình sau :
x(x + 1) ( x2 + x +1 ) = 42
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
9 tháng 2 2021
Ta có: \(\left(x+1\right)\left(x^2+x+1\right)=42\)
\(\Leftrightarrow x^3+x^2+x+x^2+x+1-42=0\)
\(\Leftrightarrow x^3+2x^2+2x-41=0\)
Đến đây thì nghiệm ra số vô tỉ đó bạn
CM
28 tháng 11 2017
a)
( x − 3 ) 2 + ( x + 4 ) 2 = 23 − 3 x ⇔ x 2 − 6 x + 9 + x 2 + 8 x + 16 = 23 − 3 x ⇔ x 2 − 6 x + 9 + x 2 + 8 x + 16 + 3 x − 23 = 0 ⇔ 2 x 2 + 5 x + 2 = 0
Có a = 2; b = 5; c = 2 ⇒ Δ = 5 2 – 4 . 2 . 2 = 9 > 0
⇒ Phương trình có hai nghiệm:
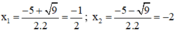
Vậy phương trình có tập nghiệm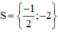 
b)
x 3 + 2 x 2 − ( x − 3 ) 2 = ( x − 1 ) x 2 − 2 ⇔ x 3 + 2 x 2 − x 2 − 6 x + 9 = x 3 − x 2 − 2 x + 2 ⇔ x 3 + 2 x 2 − x 2 + 6 x − 9 − x 3 + x 2 + 2 x − 2 = 0 ⇔ 2 x 2 + 8 x − 11 = 0
Có a = 2; b = 8; c = -11 ⇒ Δ ’ = 4 2 – 2 . ( - 11 ) = 38 > 0
⇒ Phương trình có hai nghiệm:
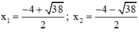
Vậy phương trình có tập nghiệm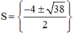 
c)
( x − 1 ) 3 + 0 , 5 x 2 = x x 2 + 1 , 5 ⇔ x 3 − 3 x 2 + 3 x − 1 + 0 , 5 x 2 = x 3 + 1 , 5 x ⇔ x 3 + 1 , 5 x − x 3 + 3 x 2 − 3 x + 1 − 0 , 5 x 2 = 0 ⇔ 2 , 5 x 2 − 1 , 5 x + 1 = 0
Có a = 2,5; b = -1,5; c = 1
⇒ Δ = ( - 1 , 5 ) 2 – 4 . 2 , 5 . 1 = - 7 , 75 < 0
Vậy phương trình vô nghiệm.
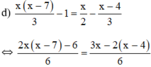
⇔ 2 x ( x − 7 ) − 6 = 3 x − 2 ( x − 4 ) ⇔ 2 x 2 − 14 x − 6 = 3 x − 2 x + 8 ⇔ 2 x 2 − 14 x − 6 − 3 x + 2 x − 8 = 0 ⇔ 2 x 2 − 15 x − 14 = 0
Có a = 2; b = -15; c = -14
⇒ Δ = ( - 15 ) 2 – 4 . 2 . ( - 14 ) = 337 > 0
⇒ Phương trình có hai nghiệm:
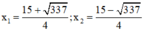
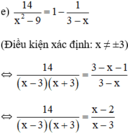
⇔ 14 = ( x - 2 ) ( x + 3 ) ⇔ 14 = x 2 - 2 x + 3 x - 6 ⇔ x 2 + x - 20 = 0
Có a = 1; b = 1; c = -20
⇒ Δ = 1 2 – 4 . 1 . ( - 20 ) = 81 > 0
Phương trình có hai nghiệm:
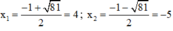
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình có tập nghiệm S = {-5; 4}.
f) Điều kiện: x≠-1;x≠4
Ta có: a= 1, b = -7, c = - 8
∆ = ( - 7 ) 2 – 4 . 1 . ( - 8 ) = 81
=> Phương trình có hai nghiệm:
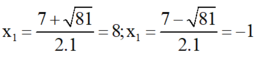
Kết hợp với diều kiện, nghiệm của phương trình đã cho là x = 8
CM
27 tháng 2 2017
a ) x = 300
b) Gợi ý: Bớt 3 ở từng phân số. Đáp số: x = 1; x = -2
CM
2 tháng 6 2018
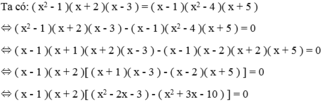
⇔ ( x - 1 )( x + 2 )( 7 - 5x ) = 0
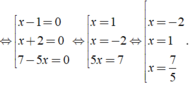
Vậy phương trình có tập nghiệm là S = { - 2; 1; 7/5 }.
CM
11 tháng 4 2019
Ta có: x 4 + 2 x 2 – x + 1 = 15 x 2 – x – 35
⇔ x 4 + 2 x 2 – x + 1 - 15 x 2 + x + 35 = 0
⇔ x 4 – 13 x 2 + 36 = 0
Đặt m = x 2 . Điều kiện m ≥ 0
Ta có: x 4 – 13 x 2 + 36 = 0 ⇔ m 2 – 13m + 36 = 0
∆ = - 13 2 – 4.1.36 = 169 – 144 = 25 > 0
∆ = 25 = 5
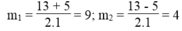
Ta có: x 2 = 9 ⇒ x = ± 3
x 2 = 4 ⇒ x = ± 2
Vậy phương trình đã cho có 4 nghiệm: x 1 = 3; x 2 = -3; x 3 = 2; x 4 = -2
PN
15 tháng 5 2021
\(|x-6|=-5x+9\)
Xét \(x\ge6\)thì \(pt< =>x-6=-5x+9\)
\(< =>x-6+5x-9=0\)
\(< =>6x-15=0\)
\(< =>x=\frac{15}{6}\)(ktm)
Xét \(x< 6\)thì \(pt< =>x-6=5x-9\)
\(< =>4x-9+6=0\)
\(< =>4x-3=0< =>x=\frac{3}{4}\)(tm)
Vậy ...
\(x\left(x+1\right)\left(x^2+x+1\right)=42\)
\(\Leftrightarrow\left(x^2+x\right)\left(x^2+x+1\right)=42\)
Đặt: \(x^2+x=v\) ta được pt mới:
\(v\left(v+1\right)=42\)
\(\Leftrightarrow\left(v-6\right)\left(v+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}v=6\\v=-7\end{matrix}\right.\)
Khi \(v=6\) ta có:
\(x^2+x-6=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)
Khi \(v=-7\) ta có:
\(x^2+x+7=0\)
\(\Leftrightarrow x^2+2x.\frac{1}{2}+\frac{1}{4}+\frac{27}{4}=0\)
\(\Leftrightarrow\left(x+\frac{1}{2}\right)^2+\frac{27}{4}=0\)
Ta có: \(\left(x+\frac{1}{2}\right)^2\ge0\forall x\)
\(\Leftrightarrow\left(x+\frac{1}{2}\right)^2+\frac{27}{4}\ge\frac{27}{4}\forall x\)
\(\Rightarrow\) Vô nghiệm
Vậy ..........
\(x\left(x+1\right)\left(x^2+x+1\right)=42\\ \left(x^2+x\right)\left(x^2+x+1\right)=42\)
Đặt \(y=x^2+x\) ta có:
\(y\left(y+1\right)=42\\\Leftrightarrow y^2+x-42=0\\ \Leftrightarrow y^2-6y+7y-42=0\\\Leftrightarrow y\left(y-6\right)+7\left(y-6\right)=0\\\Leftrightarrow \left(y+7\right)\left(y-6\right)=0\\\Leftrightarrow \left[{}\begin{matrix}y+7=0\\y-6=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}y=-7\\y=6\end{matrix}\right.\)
\(\left[{}\begin{matrix}x^2+x=6\\x^2+x=-7\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x^2+x-6=0\\x^2+x+7=0\end{matrix}\right.\Rightarrow x^2+x-6=0\left(Vix^2+x+7=0lasai\right)\\ \Leftrightarrow x^2-2x+3x-6=0\\\Leftrightarrow x\left(x-2\right)+3\left(x-2\right)=0\\ \Leftrightarrow\left(x+3\right)\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-3\\x=2\end{matrix}\right.\)Vậy tập nghiệm của phương trình là \(S=\left\{-3;2\right\}\)