B9 Tam giác ABC có \(BC=5\sqrt{5}\) ,\(AC=5\sqrt{2}\) AB=5 Tính \(\widehat{A}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
TN
1
30 tháng 8 2023
cot C=2
=>\(tanC=\dfrac{1}{cotC}=\dfrac{1}{2}\)
\(1+tan^2C=\dfrac{1}{cos^2C}\)
=>\(cos^2C=1+\dfrac{1}{4}=\dfrac{5}{4}\)
=>\(cosC=\dfrac{2}{\sqrt{5}}\) hoặc \(cosC=-\dfrac{2}{\sqrt{5}}\)
TH1: \(cosC=\dfrac{2}{\sqrt{5}}\)
=>\(\dfrac{BC^2+AC^2-AB^2}{2\cdot BC\cdot AB}=\dfrac{2}{\sqrt{5}}\)
=>\(\dfrac{5+9-AB^2}{6\sqrt{5}}=\dfrac{2}{\sqrt{5}}\)
=>\(14-AB^2=12\)
=>AB^2=2
=>\(AB=\sqrt{2}\)
TH2: \(cosC=-\dfrac{2}{\sqrt{5}}\)
=>\(\dfrac{5+9-AB^2}{6\sqrt{5}}=-\dfrac{2}{\sqrt{5}}\)
=>\(14-AB^2=\dfrac{-2}{\sqrt{5}}\cdot6\sqrt{5}=-12\)
=>AB^2=26
=>\(AB=\sqrt{26}\)
12 tháng 7 2017
a. Ta thấy \(\left(a\sqrt{5}\right)^2=\left(a\sqrt{3}\right)^2+\left(a\sqrt{2}\right)^2\Rightarrow AB^2=BC^2+AC^2\)
\(\Rightarrow\Delta ABC\)vuông tại C
b. \(\sin B=\frac{AC}{AB}=\frac{\sqrt{2}}{\sqrt{5}}=\frac{\sqrt{10}}{5};\cos B=\frac{CB}{AB}=\frac{\sqrt{3}}{\sqrt{5}}=\frac{\sqrt{15}}{5}\)
\(\tan B=\frac{AC}{AB}=\frac{\sqrt{6}}{3};\cot B=\frac{\sqrt{6}}{2}\)
\(\sin A=\cos B=\frac{\sqrt{15}}{5};\cos A=\sin B=\frac{\sqrt{10}}{5}\)
\(\tan A=\cot B=\frac{\sqrt{6}}{2};\cot A=\tan B=\frac{\sqrt{6}}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 12 2021
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}=\dfrac{5}{24}\)
\(\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=AB.AC.cosA=10a^2\)
TC
1
QT
1
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
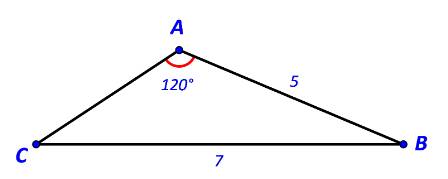
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow \sin C = \sin A.\frac{{AB}}{{BC}} = \sin {120^o}.\frac{5}{7} = \frac{{5\sqrt 3 }}{{14}}\)
\( \Rightarrow \widehat C \approx 38,{2^o}\) hoặc \(\widehat C \approx 141,{8^o}\) (Loại)
Ta có: \(\widehat A = {120^o},\widehat C = 38,{2^o}\)\( \Rightarrow \widehat B = {180^o} - \left( {{{120}^o} + 38,{2^o}} \right) = 21,{8^o}\)
Áp dụng định lí cosin trong tam giác ABC ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {5^2} + {7^2} - 2.5.7.\cos 21,{8^o}\\ \Rightarrow A{C^2} \approx 9\\ \Rightarrow AC = 3\end{array}\)
Vậy độ dài cạnh AC là 3.