Giải phương trình sau:
2x3 + 3x2 + 6x + 5 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NH
1
Những câu hỏi liên quan
PT
1
CM
3 tháng 5 2017
Chọn A
Ta có: f ' ( x ) = 6 x 2 − 6 x
Để
f ' ( x ) ≥ 0 ⇔ 6 x 2 − 6 x ≥ 0 ⇔ x ≤ 0 x ≥ 1
HN
0
CM
10 tháng 10 2019
a) Cách 1: Khai triển HĐT rút gọn được 3 x 2 + 6x + 7 = 0
Vì (3( x 2 + 2x + 1) + 4 < 0 với mọi x nên giải được x ∈ ∅
Cách 2. Chuyển vế đưa về ( x + 3 ) 3 = ( x - 1 ) 3 Û x + 3 = x - 1
Từ đó tìm được x ∈ ∅
b) Đặt x 2 = t với t ≥ 0 ta được t 2 + t - 2 = 0
Giải ra ta được t = 1 (TM) hoặc t = -2 (KTM)
Từ đó tìm được x = ± 1
c) Biến đổi được 
d) Biến đổi về dạng x(x - 2) (x - 4) = 0. Tìm được x ∈ {0; 2; 4}
CM
11 tháng 2 2019
Đặt và thực hiện phép tính ta có :
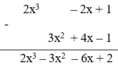
Vậy chọn đa thức thứ hai.
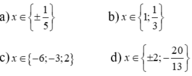
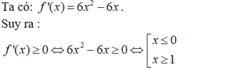
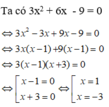
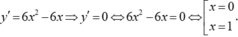
\(2x^3+3x^2+6x+5=0\)
\(\Leftrightarrow\)\(\left(2x^3+2x^2\right)+\left(x^2+x\right)+\left(5x+5\right)=0\)
\(\Leftrightarrow\)\(2x^2\left(x+1\right)+x\left(x+1\right)+5\left(x+1\right)=0\)
\(\Leftrightarrow\)\(\left(x+1\right)\left(2x^2+x+5\right)=0\)
\(\Leftrightarrow\)\(x+1=0\)
\(x=-1\)