Tìm A để M = x4 + 2019x2 -- 2018x + 4039 - A chia hết cho x2 + x + 2019
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LG
1
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 12 2021
\(x^4-9x^3+21x^2+x+a=\left(x^2-8x+15\right)\left(x^2-x-2\right)+a+30\)
\(\Rightarrow a+30=0\Rightarrow a=-30\)
PT
1
CM
24 tháng 11 2018
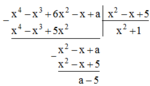
Để có phép chia hết thì số dư phải bằng 0.
Ta có: a – 5 = 0 hay a = 5.
HH
0
29 tháng 5 2023
A(x)=(1-x^n)(1+x^n)/(1-x)(1+x)
B(x)=1-x^n/1-x
A(x) chia hết cho B(x) khi 1-x^n chia hết cho 1+x
x^n+1/x+1=A(x)+(1+(-1)^n)/(x+1)
=>1-x^n chia hết cho 1+x khi và chỉ khi n=2k+1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2022
\(x^4-x^3+6x^2-x+a=x^2\left(x^2-x+5\right)+x^2-x+a\)
Do \(x^2\left(x^2-x+5\right)\) chia hết \(x^2-x+5\)
\(\Rightarrow x^2-x+a\) chia hết \(x^2-x+5\)
\(\Rightarrow a=5\)
CM
21 tháng 10 2017
Ta có
Phần dư của phép chia f(x) cho g(x) là R = (a – 1)x + b + 30
Để phép chia trên là phép chia hết thì R = 0 với mọi x
ó (a – 1)x + b + 30 = 0 với mọi x
ó a - 1 = 0 b + 30 = 0 ó a = 1 b = - 30
Vậy a = 1; b = -30
Đáp án cần chọn là: D
Z2
2
7 tháng 5 2021
`2019x^2+2020y^2-4038x+4040y+4039=0`
`<=>2019(x^2-2x+1)+2020(y^2+2y+1)=0`
`<=>2019(x-1)^2+2020(y+1)^2=0`
`<=>x=1,y=-1`