Cho tam giác ABC có AB=13cm, AC=20cm. Trên BC lấy điểm D sao cho CD=11cm và AD=13cm. Tính BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 10 2019
Do M nằm giữa A và B nên: AB = AM + MB = 13 + 11 = 24 cm
Theo hệ quả định lí Ta let ta có:
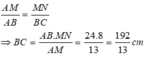
Chọn đáp án C
LD
25 tháng 3 2022
Hình bạn tự vẽ ạ.
a, Xét \(\Delta ADE\) và \(\Delta ABC\) có :
\(\dfrac{AD}{AB}=\dfrac{7}{14}=\dfrac{1}{2}\)
\(\dfrac{AE}{AC}=\dfrac{10}{20}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(=\dfrac{1}{2}\right)\)
Mà \(\widehat{A}:chung\)
\(\Rightarrow\Delta ADE\sim\Delta ABC\left(c-g-c\right)\)
b, Ta có : \(\Delta ADE\sim\Delta ABC\left(cmt\right)\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{ED}{BC}\)
hay \(\dfrac{7}{14}=\dfrac{ED}{18}\)
\(\Rightarrow ED=\dfrac{7.18}{14}=9\left(cm\right)\)
NN
29 tháng 8 2020
Xét \(\Delta ABC\)có: \(DE//BC\)\(\Rightarrow\frac{BD}{AB}=\frac{CE}{AC}\)( hệ quả của định lý Ta lét )
mà \(DB=1,5cm\); \(AB=5cm\)
\(\Rightarrow\frac{CE}{AC}=\frac{1,5}{5}=\frac{3}{10}\)\(\Rightarrow CE=\frac{3}{10}.AC\)
mà \(AC+EC=13\)\(\Rightarrow AC+\frac{3}{10}.AC=13\)
\(\Rightarrow\frac{13}{10}.AC=13\)\(\Rightarrow AC=10\left(cm\right)\)
\(\Rightarrow EC=10.\frac{3}{10}=3\left(cm\right)\)\(\Rightarrow AE=AC-EC=10-3=7\left(cm\right)\)
Vậy \(AC=10cm\); \(EC=3cm\); \(AE=7cm\)
