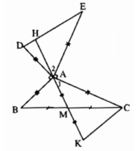
Cho tam giác ABC có góc A = 100 độ, M là trung điểm của BC. trên tia đối của MA lấy K sao cho MA = MK
a) Tính góc ABK
b) Về phía ngoài tam giác ABC vẽ các đoạn thẳng AD vuông góc và bằng AB ; AE vuông góc và bằng AC.
Chứng minh: Tam giác ABK = Tam giác DAE
c) Chứng minh: MA vuông góc với DE.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 10 2019
Có: ∠DAE + ∠DAB + ∠BAC + ∠CAE = 360o
Mà ∠DAB = ∠CAE = 90o; ∠BAC = 110o
⇒ ∠DAE = 70o
⇒ ∠DAE = ∠ACK
+) Xét ΔCAK và ΔAED có:
AC = AE (gt)
∠ACK = ∠DAE (chứng minh trên)
CK = AD (cùng = AB)
⇒ ΔCAK = ΔAED (c.g.c)
13 tháng 8 2015
b/ ta có: Góc DAE = 360 - (90 . 2) - góc A = 180 - 110 = 70 độ
từ tam giác ABM = tam giác KCM => AB = CK
Xét tam giác CAK & tam giác AED có:
KCA = DAE (bằng 70 độ)
AD = CK (bằng AB)
AC = AE (gt)
=> tam giác CAK = tam giác AED (cgc)
28 tháng 1 2016
b, vì tam giác ABM=tam giác KCM(câu a) =>AB=CK(2 cạnh tương ứng)
mà AB=AD(gt) =>KC=AD
Có DAE+DAB+EAC+BAC=3600=>DAE=3600-(DAB+EAC+BAC)
mả DAB=900(AD vuông góc vs AB-GT)
EAC=900(AE vuông góc vs AC-GT)
BAC=1100 (GT)
=>DAE=3600-(900+900+1100)=700
Có DAE=700(CMT)
ACK=700(câu a)
=>DAE=ACK(=700)
Xét tam giác CAK & tam giác AED có:
CK=AD(cmt)
CA=AE(gt)
DAE=ACK(cmt)
=>tam giác CAK=tam giác AED(c.g.c)
phần c mik k bit lm giúp nhé
26 tháng 3 2020
a) Xét \(\Delta\)ACM và \(\Delta\) KBM có:
MB = MM (gt)
MK = MA (gt)
AMC = BMK (đđ)
=> \(\Delta\)ACM = \(\Delta\)KBM (c.g.c)
=> ^ACM = ^KBM ( 2 góc tg ứng)
Vì \(\Delta\) ABC = A + B + C = 1800
=> B + C =800
=> KBM + ABC = 800
b, Ta có: ^BAC + ^CAE + ^EAD+ ^DAB = 3600
mà ^BAC=1000 ,
^CAE = ^DAB=900
=> ^EAD = 800
Vì \(\Delta\) ACM =\(\Delta\)KBM (câu a)
=> BK = AC
mà AC = AE => AE=BK
=> đpcm
c, Ta có : ^A1 + ^A2 = 900
=> ^A2 + ^E =900
Do đó : MA \(\perp\)DE