Trong mặt phẳng tọa độ Oxy, cho các điểm A(5;4), B(2;3), C(6;1). Tính các góc của tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

HP
12 tháng 2 2016
bn vẽ hình ra là sẽ thấy BAC là góc vuông =>BAC=900,mk lười vẽ quá

CM
8 tháng 9 2018
Đáp án A
Ta có khoảng cách từ A đến trục Ox bằng 6 > R.
Đường tròn (A; R) cắt trục Ox tại 2 điểm phân biệt .
Khoảng cách từ A đến trục Oy bằng 5 = R..
Do đó, đường tròn (A; R) tiếp xúc với trục Oy.
PN
1

NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 10 2019
Áp dụng công thức tọa độ trung điểm:
\(\left\{{}\begin{matrix}x_I=\frac{x_A+x_B}{2}=2\\y_I=\frac{y_A+y_B}{2}=1\end{matrix}\right.\)
\(\Rightarrow I\left(2;1\right)\)


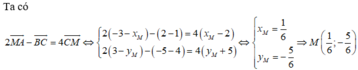
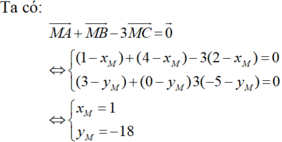
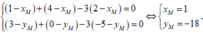
Ta vẽ \(\Delta ABC\) trên hệ trục tọa độ:
+ Xét \(\Delta ABH\) vuông tại H có:
\(AB^2=AH^2+BH^2\) (định lí Py - ta - go).
=> \(AB^2=1^2+3^2\)
=> \(AB^2=1+9\)
=> \(AB^2=10.\)
=> \(AB=\sqrt{10}\left(cm\right)\) (vì \(AB>0\)) (1).
+ Xét \(\Delta AIC\) vuông tại I có:
\(AC^2=AI^2+CI^2\) (định lí Py - ta - go).
=> \(AC^2=3^2+1^2\)
=> \(AC^2=9+1\)
=> \(AC^2=10.\)
=> \(AC=\sqrt{10}\left(cm\right)\) (vì \(AC>0\)) (2).
Từ (1) và (2) \(\Rightarrow AB=AC.\)
\(\Rightarrow\Delta ABC\) cân tại \(A\) (3).
+ Xét \(\Delta BGC\) vuông tại G có:
\(BC^2=BG^2+CG^2\) (định lí Py - ta - go).
=> \(BC^2=2^2+4^2\)
=> \(BC^2=4+16\)
=> \(BC^2=20.\)
+ Xét \(\Delta ABC\) có:
\(AB^2+AC^2=10+10\)
\(\Rightarrow AB^2+AC^2=20\)
\(BC^2=20\)
\(\Rightarrow AB^2+AC^2=BC^2\left(=20\right).\)
\(\Rightarrow\Delta ABC\) vuông tại \(A\) (định lí Py - ta - go đảo) (4).
Từ (3) và (4) \(\Rightarrow\Delta ABC\) vuông cân tại A.
\(\Rightarrow\left\{{}\begin{matrix}\widehat{BAC}=90^0\\\widehat{ABC}=\widehat{ACB}=45^0\end{matrix}\right.\) (tính chất tam giác vuông cân).
Vậy các góc của tam giác \(ABC\) là: \(\widehat{BAC}=90^0;\widehat{ABC}=\widehat{ACB}=45^0.\)
Chúc em học tốt!