Cho hai điện trở R1 = 60(ôm) và R2 = 40(ôm) được mắc song song với nhau vào giữa hai điểm A, B có hiệu điện thế luôn không đổi U = 120V. Tính:
a. Điện trở tương đương của đoạn mạch. (Không cần làm)
b. Cường độ dòng điện qua mỗi điện trở và qua mạch chính. ( Không cần làm)
c. Giả sử R2 là một biến trở có sợi dây được làm bằng constantan với điện trở suất bằng 0,5.10-6(ôm)m, có 150 vòng quấn quanh một lõi sứ trụ tròn đường kính 2,5cm. Hãy tính tiết diện dây dẫn dùng làm biến trở. ( CÂU C GIÚP VỚI Ạ)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Điên trở tương đương của đoạn mạch này là :
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{60.12}{60+12}=10\Omega\)
b. CĐDĐ qua mạch chính là :
\(I=\dfrac{U}{R}=\dfrac{2,4}{10}=0,24A\)
Vì \(R_1\)//\(R_2\) nên :
\(U=U_1=U_2=2,4V\)
CĐDĐ qua các đoạn mạch rẽ là :
\(I_1=\dfrac{U_1}{R_1}=\dfrac{2,4}{60}=0,04A\)
\(\Rightarrow I_2=0,24-0,04=0,2A\)
c. Vì điện trở \(R_3\) nt ( \(R_1\)//\(R_2\)) nên điện trở tương đương toàn mạch là :
\(R_{123}=R_{12}+R_3=10+16=26\Omega\)
\(\Rightarrow\) CĐDĐ qua mạch chính là :
\(I=\dfrac{U}{R_{123}}=\dfrac{2,4}{26}\approx0,1A\)
Vậy : a. Điện trở tương đương của đoạn mạch \(R_1\)//\(R_2\) là \(10\Omega\)
b. I = 0,24A ; \(I_1=0,04A\) ; \(I_2=0,2A\)
c. \(I_{123}\) = 0,1A

Điện trở tương đương của đoạn mạch là:
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{30.60}{30+60}=20\left(\Omega\right)\)
Do mắc song song nên \(U=U_1=U_2=30V\)
Cường độ dòng điện chạy qua mạch chính và mỗi mạch rẽ:
\(\left\{{}\begin{matrix}I=\dfrac{U}{R_{tđ}}=\dfrac{30}{20}=1,5\left(A\right)\\I_1=\dfrac{U_1}{R_1}=\dfrac{30}{30}=1\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{30}{60}=0,5\left(A\right)\end{matrix}\right.\)
Điện trở tương đương lúc này là:
\(R_{tđ}=R_{12}+R_3=20+40=60\left(\Omega\right)\)
Do mắc nối tiếp nên \(I=I_{12}=I_3=1,5\left(A\right)\)
Nhiệt năng đoạn mạch tiêu thụ trong 30ph:
\(A=P.t=I^2.R.t=1,5^2.60.30.60=243000\left(J\right)\)
Nhiệt lượng tỏa ra của R3 trong 30ph:
\(Q_{tỏa_3}=A_3=I_3^2.R_3.t=1,5^2.40.30.60=162000\left(J\right)\)

\(a,R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{60.40}{60+40}=24\left(\Omega\right)\)
\(I_m=\dfrac{U}{R_{tđ}}=\dfrac{12}{24}=0,5\left(\Omega\right)\)
\(b,P_1=\dfrac{U}{R_1}=\dfrac{12^2}{60}=2,4\left(W\right)\)
\(P_2=\dfrac{U^2}{R}=\dfrac{12^2}{40}=3,6\left(W\right)\)
\(P_m=U.I=12.0,5=6\left(W\right)\)

Tóm tắt:
R1 = 12\(\Omega\)
R2 = 6\(\Omega\)
R1//R2
U=12V
a) Rtd =?\(\Omega\)
b) I=? A
Giải:
Vì R1 mắc song song với R2
Điện trở tương đương của đoạn mạch là:
\(R_{td}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{12.6}{12+6}=4\Omega\)
b) Vì R1 mắc song song với R2
Ta có: U= U1=U2 =12V
Cường độ dòng điện chạy qua đoạn mạch chính là:
\(I=\dfrac{U}{R_{td}}=\dfrac{12}{4}=3\left(A\right)\)
Đáp số: a) 4\(\Omega\)
b) 3A
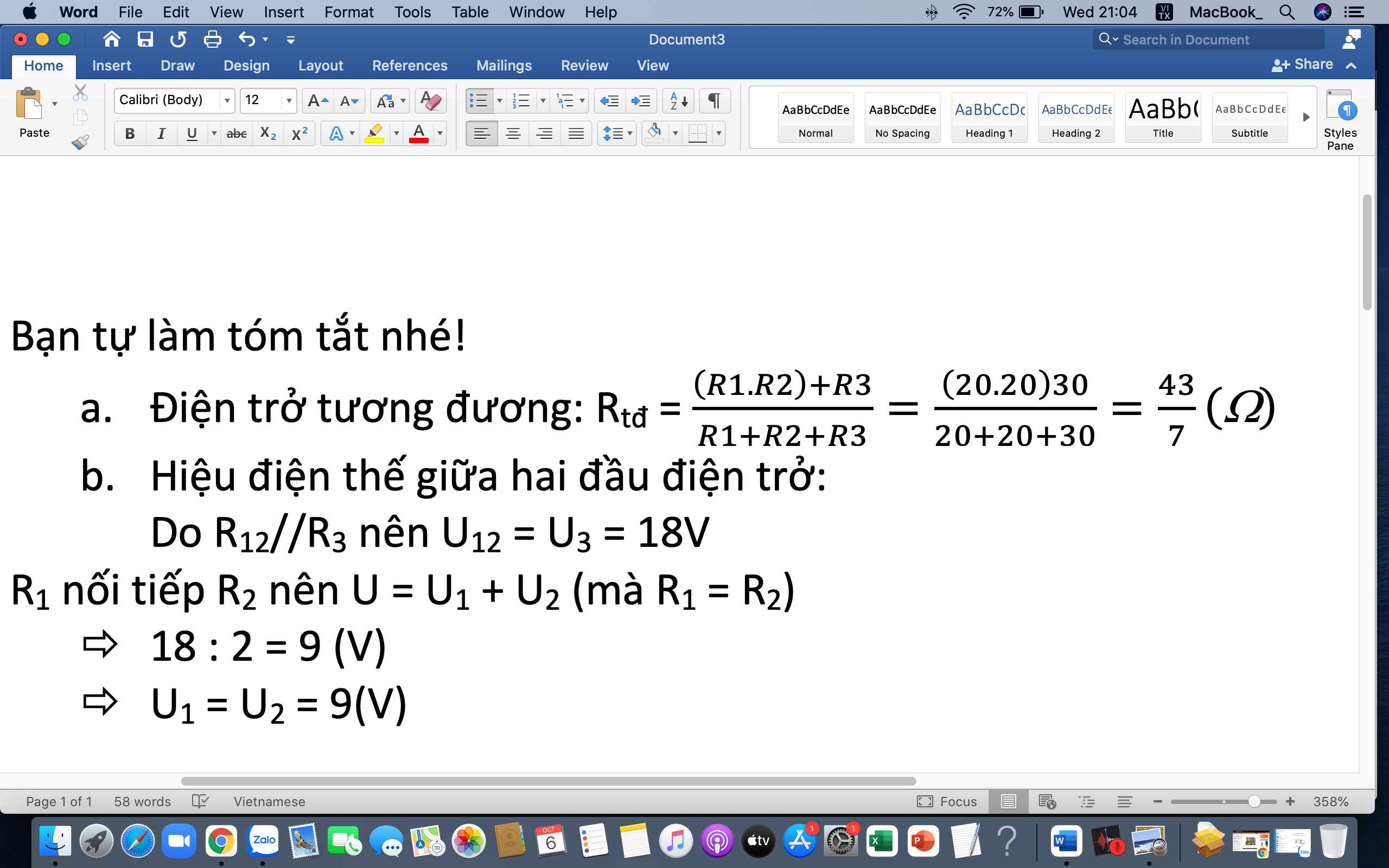

Giúp e với ạ