Một viên đạn đang bay ngang với vận tốc 300m/s thì nổ nổ thf 2 mảnh. Mảnh 1 có khối lượng 5 kg bay theo phương thẳng đứng hướng lên vs vận tốc 400√3 m/s ; mảnh 2 có khối lượng 15kg. Xác định hướng và độ lớn vận tốc của mảnh 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo đl bảo toàn động lượng :
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
=> \(p_2=\sqrt{p^2-p_1^2}\)
\(\Leftrightarrow m_2v_2=\sqrt{\left(mv\right)^2-\left(m_1v_1\right)^2}\)
=> \(v_2=\frac{\sqrt{\left(mv\right)^2-\left(m_1v_1\right)^2}}{m_2}=\frac{\sqrt{\left(300.20\right)^2-\left(5.400\sqrt{3}\right)^2}}{15}\approx326,6\left(m/s\right)\)

Theo định luật bảo toàn động lượng :
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
=> \(p_2=\sqrt{p_1^2-p^2}\)
<=> \(m_2v_2=\sqrt{\left(m_1v_1\right)^2-\left(mv\right)^2}\)
=>

Coi hệ trên là hệ kín, ta có áp dụng bảo toàn động lượng có: \(\overrightarrow{P}=\overrightarrow{P_1}+\overrightarrow{P_2}\)
\(\Rightarrow P_2^2=P_1^2+P^2\Leftrightarrow\left(m_2v_2\right)^2=\left(m_1v_1\right)^2+\left(\left(m_1+m_2\right)v\right)^2\)
\(\Leftrightarrow\left(20v_2\right)^2=\left(10.519\right)^2+\left(30.300\right)^2\)
\(\Rightarrow v_2=519,4615\) (m/s)
Ta có: \(P_1=10.519=5190N\) và \(P_2=20.519,4615=10389,23N\)
Vậy mảnh hai rơi xéo xuống một góc arcsin(5190/10389,23)\(\approx30^0\)so với phương ngang

Xét hệ gồm 2 mảnh đạn trong thời gian nổ, đây là hệ kín nên ta áp dụng định luật bảo toàn động lượng: \(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p_h}\)
Trong đó: \(p_h=mv=195\left(kg.m/s\right)\)
\(p_1=m_1v_1=90\sqrt{3}\left(kg.m/s\right)\)
Áp dụng định lý hàm cos: \(p_2=\sqrt{p_1^2+p_h^2-2p_1p_h\cos\left(60^0\right)}\) => v2=p2/m2 =..... tự tính
Gọi \(\beta\) là góc hợp bởi phương ngang và mảnh thứ 2 ta có: \(\cos\beta=\dfrac{p_h^2+p_1^2-p_2^2}{2p_hp_1}=.......\) tự tính nốt :D

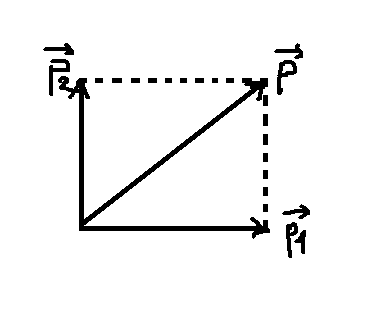
a)Vận tốc viên đạn trước khi nổ:
\(tan45^o=\dfrac{p}{p_1}=\dfrac{m\cdot v}{m_1\cdot v_1}=\dfrac{2\cdot v}{0,5\cdot400}\)
\(\Rightarrow v=100\)m/s
Vận tốc mảnh đạn lớn:
\(sin45^o=\dfrac{p_1}{p_2}=\dfrac{m_1\cdot v_1}{m_2\cdot v_2}=\dfrac{0,5\cdot400}{\left(2-0,5\right)\cdot v_2}\)
\(\Rightarrow v_2=188,56\)m/s

Gọi \(\overrightarrow{v};\overrightarrow{v_1};\overrightarrow{v_2}\) lần lượt là vận tốc của viên đạn ban đầu, của mảnh đạn 1kg và mảnh đạn 2kg sau khi bắn
Động lượng ban đầu của viên đạn là
\(\overrightarrow{p_0}=3\overrightarrow{v}\)
Động lượng sau của hệ là
\(\overrightarrow{p_s}=\overrightarrow{v_1}+2\overrightarrow{v_2}\)
Do động lượng được bảo toàn nên
\(\overrightarrow{p_0}=\overrightarrow{p_s}\) ⇒ \(3\overrightarrow{v}=\overrightarrow{v_1}+2\overrightarrow{v_2}\)
⇒ \(\overrightarrow{v_1}=3\overrightarrow{v}-2\overrightarrow{v_2}\)
⇒ v12 = 9.v2 + 4v22 - 12 . v . v2 . cos (45)
⇒ v12 = 9 . 472 + 4.502 - 12 . 47 . 50 . \(\dfrac{\sqrt{2}}{2}\)
⇒ v1 = 99,7 (m/s)
\(3\overrightarrow{v}=\overrightarrow{v_1}+2\overrightarrow{v_2}\)
⇒ \(2\overrightarrow{v_2}=3\overrightarrow{v}-\overrightarrow{v_1}\)
⇒ cos \(\left(\overrightarrow{v};\overrightarrow{v_1}\right)\) = 0.789
⇒ \(\left(\overrightarrow{v};\overrightarrow{v_1}\right)\) = 37054'
Vậy mảnh đạn 1 bay theo chiều dương và hợp với phương thẳng đứng 1 góc 37054' có độ lớn là 99,7 m/s



Bạn ơi nhầm đề không ạ
Không đâu