tìm hai số nguyên, biết hiệu của hai số đó là 99. Nếu chía số bé cho 3 và số lớn cho11 thì thương thứ nhất hơn thương thứ hai 7 đơn vị. Biết các phép chia nói trên là các phép chia hết.

LN

LÊ NGỌC LINH

9 tháng 2 2020

tìm hai số nguyên, biết hiệu của hai số đó là 99. Nếu chía số bé cho 3 và số lớn cho11 thì thương thứ nhất hơn thương thứ hai 7 đơn vị. Biết các phép chia nói trên là các phép chia hết. ...

Đọc tiếp

#Toán lớp 9

1

TT

Trần Thị Như Ý

10 tháng 2 2020

https://i.imgur.com/vE7wJDP.jpg

Đúng(0)

LN

LÊ NGỌC LINH

11 tháng 2 2020 - olm

tìm hai số nguyên, biết hiệu của hai số đó là 99. Nếu chia số bé cho 3 và số lớn cho 11 thì thương thứ nhất hơn thương thứ hai 7 dơn vị. Biết các phép chia nói trên là các phép chia hết.

#Toán lớp 9

1

NN

Ngọc Nguyễn

11 tháng 2 2020

Gọi số lớn là: x ( x\(\in\)N^*)

số bé là: y ( y\(\in\)N*)

\(\Rightarrow\)x - y = 99 (1)

Vì khi chia số bé cho 3 và số lớn cho 11 thì thương thứ nhất hơn thương thứ hai 7 đơn vị

\(\Rightarrow\frac{-x}{11}+\frac{y}{3}=7\)(2)

Từ (1) và (2) ta có hệ phương trình:

\(\hept{\begin{cases}x-y=99\\\frac{-x}{11}+\frac{y}{3}=7\end{cases}\Leftrightarrow\hept{\begin{cases}x=165\\y=66\end{cases}}}\)

VẬY...

Đúng(0)

PT

Pham Trong Bach

10 tháng 8 2017

Hai số nguyên dương có tỉ số giữa số thứ nhất và số thứ hai bằng 3/5. Nếu lấy số thứ nhất chia cho 9, số thứ hai chia cho 6 thì thương của phép chia số thứ nhất cho 9 bé hơn thương của phép chia số thứ hai cho 6 là 3 đơn vị. Tìm hai số đó biết rằng các phép chia nói trên đều là phép chia hết.

#Toán lớp 8

1

CM

Cao Minh Tâm

10 tháng 8 2017

Gọi a (a ∈ N *) là số thứ nhất. Ta có số thứ hai là 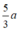Bài 47 trang 14 SBT Toán 8 Tập 2

Thương phép chia số thứ nhất cho 9 là a/9

Thương phép chia số thứ hai cho 6 là: 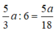Bài 47 trang 14 SBT Toán 8 Tập 2

Thương thứ nhất bé hơn thương thứ hai là ba đơn vị nên ta có phương trình:

5a/18 - a/9 = 3

⇔ 5a/18 - 2a/18 = 54/18

⇔ 5a – 2a = 54

⇔ 3a = 54 ⇔ a = 18 (thỏa mãn)

Vậy số thứ nhất là 18, số thứ hai là 5/3.18 = 30.

Đúng(0)

NT

nguyễn thị mai hương

2 tháng 2 2019 - olm

Hai số nguyên dương có tỉ số giữa số thứ nhất và số thứ hai bằng 3/5 . nếu lấy số thứ 1 chia cho 9 , số thứ 2 chia cho 6 thì thương của phép chia số thứ nhất cho 9 bé hơn thương của phép chia số thứ hai cho 6 là 3 đơn vị . tìm hai số đó biết các phép chia nói trên đều là phép chia hết .

#Toán lớp 8

3

D

dyrcraa

11 tháng 2 2020

gọi số thứ 1 là x ĐK x,y >0

--------------2----y

do tỉ số giữa 2 số là 3/5 => 5x=3y (1)

số thứ 1 chia 9 bé hơn số thứ 2 chia 6 là 3 đơn vị nên ta có phương trình

y/6 - x/9 = 3 (2)

từ (1) và (2) ta có hệ phương trình

........

x=18 y=30

vậy ........

Đúng(0)

NQ

Nguyễn Quang Khương

24 tháng 4 2020

cau ntn

Đúng(0)

SG

Sách Giáo Khoa

4 tháng 5 2017

Hai số nguyên dương có tỉ số giữa số thứ nhất và số thứ hai bằng \(\dfrac{3}{5}\). Nếu lấy số thứ nhất chia cho 9, số thứ hai chia cho 6 thì thương của phép chia số thứ nhất cho 9 bé hơn thương của phép chia số thứ hai cho 6 là 3 đơn vị. Tìm hai số đó biết rằng các phép chia nói trên đều là phép chia hết ?

#Toán lớp 8

1

NT

Nguyễn Trần Thành Đạt

5 tháng 5 2017

+) Gọi số thứ nhất (ban đầu) là x. (x: nguyên, dương)

Khi đó số thứ hai (ban đầu) là \(\dfrac{3}{5}x\)

+) Số thứ nhất sau khi chia cho 9 gọi là \(\dfrac{x}{9}\)

Số thứ hai sau khi chia cho 6 gọi là \(\dfrac{\dfrac{3}{5}x}{6}\)

Vì: thương số thứ nhất chia cho 9 bé hơn thương số thứ hai chia cho 6 là 3 đơn vị nên ta có phương trình:

\(\dfrac{x}{9}+3=\dfrac{\dfrac{3}{5}x}{6}\\ < =>\dfrac{2x}{18}+\dfrac{54}{18}=\dfrac{\dfrac{9}{5}x}{18}\\ < =>2x+54=\dfrac{9}{5}x\\ < =>2x-\dfrac{9}{5}x=-54\\< =>\dfrac{1}{5}x=-54\\ =>x=\dfrac{-54}{\dfrac{1}{5}}=-270\left(loại\right)\)

Vậy: Không thỏa mãn yêu cầu đề bài.

Đúng(0)

NH

Nguyễn Hải Minh

7 tháng 4 2020 - olm

Hai số nguyên dương có tỉ số giữa số thứ nhất và số thứ hai là 4/7. Nếu lấy số thứ nhất chia cho 4, số thứ hai chia cho 5 thì thương thứ nhất bé hơn thương thứ hai 2 đơn vị. Tìm hai số đó, biết rằng các phép chia trên đều là phép chia hết.

Số bé là

Số lớn là

#Toán lớp 8

1

NN

Nobi Nobita

7 tháng 4 2020

Gọi 2 số cần tìm lần lượt là a, b \(\left(a,b\inℕ^∗\right)\)

Tỉ số giữa số thứ nhất và số thứ 2 là \(\frac{4}{7}\)\(\Rightarrow\frac{a}{b}=\frac{4}{7}\)\(\Rightarrow\frac{a}{4}=\frac{b}{7}\)

Đặt \(\frac{a}{4}=\frac{b}{7}=k\left(k\inℕ^∗\right)\)\(\Rightarrow a=4k\)và \(b=7k\)

Nếu lấy số thứ nhất chia cho 4, số thứ 2 chia cho 5 thì thương số thứ nhất bé hơn thương thứ hai 2 đơn vị

\(\Rightarrow\)Ta có phương trình: \(\frac{7k}{5}-\frac{4k}{4}=2\)

\(\Leftrightarrow\frac{28k}{20}-\frac{20k}{20}=\frac{40}{20}\)\(\Leftrightarrow8k=40\)\(\Leftrightarrow k=5\)( thoả mãn điều kiện )

\(\Rightarrow a=4.5=20\); \(b=5.7=35\)

Vậy số bé là 20 và số lớn là 35

Đúng(0)

MN

Mickey Nhi

21 tháng 2 2016 - olm

Hai số nguyên dương có tỉ số giữa số thứ nhất và số thứ hai bằng \(\frac{3}{5}\). Nếu lấy số thứ nhất chia cho 9, số thứ hai cho 6 thì thương của phép chia số thứ nhất cho 9 bé hơn thương của phép chia số thứ hai cho 6 là 3 đơn vị. Tìm hai số đó, biết rằng các phép chia nói trên đều là phép chia hết.

#Toán lớp 8

0

NQ

Ngọc Quỳnh Anh

21 tháng 4 2020 - olm

Hai số nguyên dương có tỉ số giữa số thứ nhất và số thứ hai là 5/8. Nếu lấy số thứ nhất chia cho 5, số thứ hai chia cho 6 thì thương thứ nhất bé hơn thương thứ hai 2 đơn vị. Tìm hai số đó, biết rằng các phép chia trên đều là phép chia hết.

số bé là:

số lớn là:

#Toán lớp 8

0

VG

VŨ GIA KHANG

23 tháng 3 2020 - olm

Hai số nguyên dương có tỉ số giữa số thứ nhất và số thứ hai là 4/7. Nếu lấy số thứ nhất chia cho 4, số thứ hai chia cho 5 thì thương thứ nhất bé hơn thương thứ hai 2 đơn vị. Tìm hai số đó, biết rằng các phép chia trên đều là phép chia hết.

#Toán lớp 8

1

DD

✫¸.•°*”˜˜”*°•✫ Ṱђầภ Ḉђết ✫•°*”˜˜”*°...

23 tháng 3 2020

Bài làm

Gọi số thứ nhất là 4.a = 4a

Số thứ hai là 7.a = 7a

Vì là số nguyên dương nên a>0

Ta có phương trình: 4a/4 - 7a/9 = 2

Hay a - 7a/9 = 2

<=> 36a/36 - 28a/36 = 2

<=> (36a-28a)/2 = 2

<=> 4a/2 = 2

<=> 2a = 2

<=> a = 1

Mà a > 0

=> a = 1 thoả mãn

Ta có: số thứ nhất là: 4a = 4 .1 = 4

Số thứ hai là: 7a = 7 .1 = 7

V

Đúng(0)

NQ

Ngọc Quỳnh Anh

21 tháng 4 2020 - olm

Hai số nguyên dương có tỉ số giữa số thứ nhất và số thứ hai là 5/8 Nếu lấy số thứ nhất chia cho 5, số thứ hai chia cho 6 thì thương thứ nhất bé hơn thương thứ hai 2 đơn vị. Tìm hai số đó, biết rằng các phép chia trên đều là phép chia hết

#Toán lớp 8

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP