Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


N:tập hợp các số tự nhiên
N*:tập hợp các số tự nhiên khác 0.
Z:tập hợp các số nguyên
S:tập hợp các nghiệm
Q:tập hợp các số
T:tập hợp các số và có dạng số:T={a2=-1}
Q:tập hợp tất cả các số
T:tập hợp tất cả các số và thêm các số có dạng:a2=-k(k thuộc N)

là số viết đc đướ dạng số thập phân vô hạn ko tuần hoàn
kí hiệu là I

định dạng kí tự là thay đổi dáng vẻ của một hay một nhóm kí tự.

- Dữ liệu số: + Tự động căn lề phải trong ô tính.
+ Dấu "," để ngăn cách hàng nghìn, hàng triệu, dấu "." để năn cách phần nguyên và phần thập phân.
- Dữ liệu kí tự: + Tự động căn lề trái trong ô tính.
+ Các kí tự có thể: chữ cái, các kí hiệu

nước vô tình triệu năm không tắm
mây vô tình mây bay mãi chẳng ngưng
trăng vô tình trăng giỡn mặt với gió
người vô tình có chó mới thương
theo em bài thơ dzô cùng sâu sắc


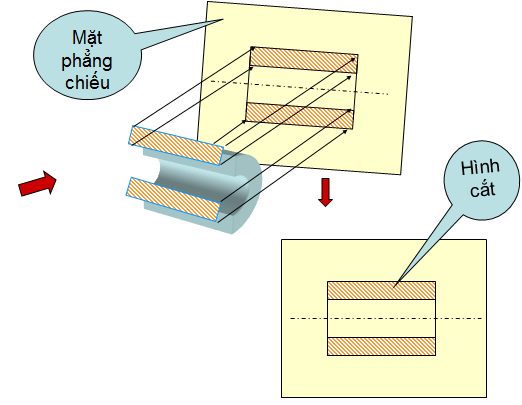
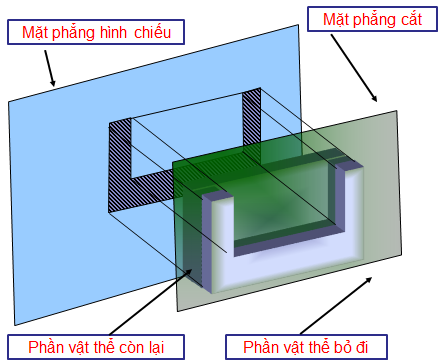
Khái niệm
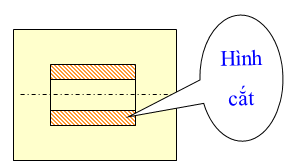
Hình cắt là hình biểu diễn phần vật thể ở phía sau mặt phẳng cắt.
Trên bản vẽ kĩ thuật thường dùng hình cắt để biểu diễn hình dạng bên trong của vật thể.
Phần vật thể bị mặt phẳng cắt cắt qua được kẻ bằng nét gạch gạch.

Bước 1: Chọn phần văn bản cần định dạng kí tự.
Bước 2: Nháy chuột trái vào các nút lệnh trên thanh công cụ định dạng thích hợp.
Các nút lệnh định dạng gồm:
+ Định dạng phông chữ;
+ Định dạng cỡ chữ;
+ Định dạng kiểu chữ;
+ Định dạng màu chữ.
Chúc bạn học tốt!
Bước 1: Chọn phần văn bản cần định dạng kí tự .
Bước 2: Nháy chuột trái vào các nút lệnh trên thanh công cụ định dạng thích hợp .
Các nút lệnh định dạng gồm :
`->` Định dạng phông chữ;
`->` Định dạng cỡ chữ;
`->` Định dạng kiểu chữ;
`->` Định dạng màu chữ.

Trong toán học, số vô tỉ là số thực không phải là số hữu tỷ, nghĩa là không thể biểu diễn được dưới dạng tỉ số 


Tập hợp số vô tỉ ký hiệu là
Trong toán học, số vô tỉ là số thực không phải là số hữu tỷ, nghĩa là không thể biểu diễn được dưới dạng tỉ số {\displaystyle {\frac {a}{b}}}


{\displaystyle \mathbb {I} =\left\{x|x\neq {\frac {m}{n}}\forall m\in \mathbb {Z} ,\forall n\in \mathbb {Z^{*}} \right\}}

