Câu 1: Cho tam giác ABC, một đường thẳng // với BC cắt AB và AC lần lượt tại D và E. Khẳng định nào sau đây đúng
A.\(\frac{DC}{DB}=\frac{EA}{EC}\) B. DC.DB=EC.EA
C. DC.EC=DB.EA D. DC.ea=DB.EC
Câu 2: Cho tam giác ABC, MN//BC với M nằm giữa A và B, N nằm giữa A và C. Biết AN=2cm, AB=3AM. Kết quả nào đúng
A. AC=6cm B. CN=3cm C. AC=9cm D. CN=1,5cm
Câu3: Cho tam giác ABC, AB=14cm, AC =21cm. AD là phân giác của góc A. Biết BD=8cm. Độ dài cạnh BC là
A. 15cm B. 18cm C. 20cm D. 22cm
Câu 4: Cho tam giác MNK, NS là phân giác góc MNK. Biết MN=3cm, NK=5cm, MS=1,5cm. Ta có SK=
A. 2,5cm B. 0,1cm C.0,4cm D.10cm



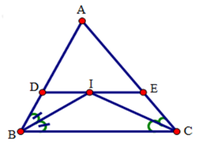
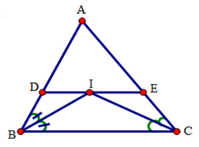
Câu 1: Cho tam giác ABC, một đường thẳng // với BC cắt AB và AC lần lượt tại D và E. Khẳng định nào sau đây đúng
A.DCDB=EAECDCDB=EAEC B. DC.DB=EC.EA
C. DC.EC=DB.EA D. DC.ea=DB.EC
Câu 2: Cho tam giác ABC, MN//BC với M nằm giữa A và B, N nằm giữa A và C. Biết AN=2cm, AB=3AM. Kết quả nào đúng
A. AC=6cm B. CN=3cm C. AC=9cm D. CN=1,5cm
Câu3: Cho tam giác ABC, AB=14cm, AC =21cm. AD là phân giác của góc A. Biết BD=8cm. Độ dài cạnh BC là
A. 15cm B. 18cm C. 20cm D. 22cm
Câu 4: Cho tam giác MNK, NS là phân giác góc MNK. Biết MN=3cm, NK=5cm, MS=1,5cm. Ta có SK=
A. 2,5cm B. 0,1cm C.0,4cm D.10cm