hai lớp 9A và 9B có tất cả 76 học sinh . Học kì I vừa qua hai lớp có 14 học sinh giỏi . Trong đó số học sinh của lớp 9A chiếm 1/6 học sinh của lóp , còn 9B chiếm 20% số học sinh của cả lớp . Hỏi hai lớp có bao nhiêu học sinh
giúp mình với mn oiiii
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
30 tháng 3 2020
Gọi số hs lớp 9A là x => số hsg của lớp 9A là \(\frac{x.60}{100}\)
Gọi số hs lớp 9B là y => số hsg của lớp 9b là \(\frac{y.75}{100}\)
=> Ta có pt (1) \(\frac{60x}{100}+\frac{75y}{100}=51\Leftrightarrow12x+15y=1020\)
Ta có hệ PT
\(\hept{\begin{cases}x+y=76\\12x+15y=1020\end{cases}}\)
Giải hệ PT trên
31 tháng 1 2021
Gọi a(bạn) là số học sinh của lớp 9A(Điều kiện: \(a\in Z^+\))
Gọi b(bạn) là số học sinh của lớp 9B(Điều kiện: \(b\in Z^+\))
Vì khi chuyển ba học sinh từ 9A sang lớp 9B thì số học sinh hai lớp bằng nhau nên ta có phương trình:
\(a-3=b+3\)
\(\Leftrightarrow a-3-b-3=0\)
\(\Leftrightarrow a-b-6=0\)
hay a-b=6(1)
Vì khi chuyển 5 học sinh từ 9B sang lớp 9A thì số học sinh lớp 9B bằng \(\dfrac{11}{19}\)số học sinh lớp 9A nên ta có phương trình:
\(b-5=\dfrac{11}{19}\cdot\left(a+5\right)\)
\(\Leftrightarrow b-5-\dfrac{11}{19}a-\dfrac{55}{19}=0\)
\(\Leftrightarrow\dfrac{-11}{19}a+b=\dfrac{150}{19}\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}a-b=6\\-\dfrac{11}{19}a+b=\dfrac{150}{19}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{8}{19}a=\dfrac{264}{19}\\a-b=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=33\left(nhận\right)\\b=a-6=33-6=27\left(nhận\right)\end{matrix}\right.\)
Vậy: Số học sinh lớp 9A là 33 bạn
Số học sinh lớp 9B là 27 bạn
CM
5 tháng 5 2019
Đáp án B
Gọi x, y lần lượt là số học sinh của lớp 9A và lớp 9B (x, y ∈ N*; x, y < 82)
Tổng số học sinh của hai lớp là 82 ⇒ x + y = 82 (1)
Mỗi học sinh lớp 9A và 9B lần lượt trồng được 3 cây và 4 cây nên tổng số cây hai lớp trồng là 3x + 4y (cây). Theo bài ra ta có 3x + 4y = 288 (2)
Từ (1) và (2) ta có hệ phương trình:
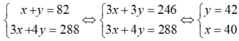(thỏa mãn)
Vậy số học sinh lớp 9A và 9B lần lượt là 40 và 42.
7 tháng 6 2018
Gọi số học sinh giỏi của lớp 9C là x ( học sinh ) ( \(x\in\)N* )
Tổng số học sinh của lớp 9A ; 9B ; 9C là: \(x+75\)( học sinh )
Tổng số học sinh giỏi của lớp 9A ; 9B ; 9C là: \(27+\frac{x}{5}\)
Theo đề bài ta có phương trình:
\(27+\frac{x}{5}=\frac{30\left(x+75\right)}{100}\)
\(\Leftrightarrow270+2x=3x+225\)
\(\Leftrightarrow x=270-225=45\)( học sinh )
Vậy số học sinh giỏi lớp 9C là 45 học sinh
2 tháng 2 2021
Có thêm 4 học sinh thì tăng từ 40% lên 48%
\(\Rightarrow\) 4 học sinh tương đương với 8% số học sinh cả lớp
\(\Rightarrow\) Số học sinh cả lớp là: \(\dfrac{4}{8\%}=50\) (học sinh)
2 tháng 2 2021
Đề hình như sai hoặc em lag
+Nếu số học sinh ở học kì 1 là 50 thì khi sang học kì 2 sẽ là 54, đồng nghĩa với việc 48% số học sinh giỏi ở học kì 2 sẽ là 25,92 học sinh.
+Nếu số học sinh ở kì 2 là 50 thì ở học kì 1 sẽ là 46, cũng có nghĩa là 40% số học sinh ở kì 1 sẽ là 18,4 học sinh
@@
1 tháng 5 2017
a) Số HS nam chiếm số phần trăm số HS cả lớp là : \(\frac{27}{45}.100\%=60\%\)
b) Số HSTB của lớp 6D là : \(45.\frac{7}{15}=21\left(HS\right)\)
số HSK của lớp 6D la : ( 45 - 21 ) . 5/8 = 15 ( HS )
Số HSG của lớp 6D là : 45 - 21 - 15 = 9 ( HS )
Dap so : a) 60 %
b) 9 HSG
23 tháng 11 2023
Gọi số học sinh giỏi của lớp 9A và số học sinh của lớp 9A lần lượt là x(bạn), y(bạn)
(Điều kiện: \(x,y\in Z^+\))
Cuối học kì 1, số học sinh giỏi của lớp 9A bằng 20% số học sinh cả lớp nên ta có: \(x=20\%y=0,2y\)(1)
Sang học kì 2, lớp có thêm 2 bạn đạt học sinh giỏi nên số học sinh giỏi kì 2 bằng số học sinh cả lớp nên ta có:
x+2=y(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x=0,2y\\x+2=y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}0,2y+2=y\\x=0,2y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-0,8y=-2\\x=0,2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2,5\\x=0,2\cdot2,5=0,5\end{matrix}\right.\)(loại)
=>Đề sai rồi bạn
23 tháng 2 2020
Vậy lớp 9A hơn lớp 9B 10 học sinh .
Lớp 9A có số học sinh là :
(70 + 10 ):2=40(học sinh )
Lớp 9B có số học sinh là :
(70 - 10 ):2=30(học sinh )
Gọi số học sinh lớp 9a là: x ( x,y\(\in\)N* ) ( học sinh )
9b là: y
\(\Rightarrow x+y=76\)(1)
Số học sinh giỏi lớp 9a là: \(\frac{1}{6}x\)hs
9b là: \(\frac{1}{5}y\)hs
\(\Rightarrow\frac{1}{6}x+\frac{1}{5}y=14\)(2)
Từ (1) và (2) ta có hệ phương trình:
\(\hept{\begin{cases}x+y=76\\\frac{1}{6}x+\frac{1}{5}y=14\end{cases}\Leftrightarrow\hept{\begin{cases}x=36\\y=40\end{cases}}}\)
Vậy...