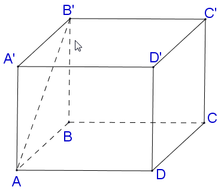
Cho lăng truh đứng ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật, biết A'B tạo với đáy một góc 300 và AB = 2a, AD = 4a. Tính thể tích khối lăng trụ đã cho theo a.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
A
4 tháng 5 2023
Phát biểu nào sau đây là đúng?
A. Các mặt bên của hình lăng trụ đứng là hình chữ nhật
B. Các mặt bên của hình lăng trụ đứng là hình thang cân
C. Các mặt đáy của hình lăng truh đứng là các hình chữ nhật
D. Các mặt đáy của hình lăng trụ đứng là các hình tam giác
4 tháng 5 2023
Phát biểu nào sau đây là đúng?
A. Các mặt bên của hình lăng trụ đứng là hình chữ nhật
B. Các mặt bên của hình lăng trụ đứng là hình thang cân
C. Các mặt đáy của hình lăng truh đứng là các hình chữ nhật
D. Các mặt đáy của hình lăng trụ đứng là các hình tam giác
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 4 2022
Đặt \(x=AA'\)
Ta có: \(\overrightarrow{AB'}=\overrightarrow{AA'}+\overrightarrow{AB}\) ; \(\overrightarrow{BD'}=\overrightarrow{BB'}+\overrightarrow{BD}=\overrightarrow{BB'}+\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{AA'}-\overrightarrow{AB}+\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{AB'}.\overrightarrow{BD'}=\left(\overrightarrow{AA'}+\overrightarrow{AB}\right)\left(\overrightarrow{AA'}-\overrightarrow{AB}+\overrightarrow{BC}\right)\)
\(=AA'^2+\overrightarrow{AA'}\left(-\overrightarrow{AB}+\overrightarrow{BC}\right)+\overrightarrow{AB}.\overrightarrow{AA'}-AB^2+\overrightarrow{AB}.\overrightarrow{BC}\)
\(=x^2-a^2+AB.BC.cos120^0\)
\(=x^2-a^2-\dfrac{a^2}{2}=x^2-\dfrac{3a^2}{2}=0\)
\(\Rightarrow x=\dfrac{a\sqrt{6}}{2}\)
\(V=\dfrac{a\sqrt{6}}{2}.2.\dfrac{a^2\sqrt{3}}{4}=\dfrac{3a^3\sqrt{2}}{4}\)
20 tháng 10 2021
\(AA'=\dfrac{2a}{\sqrt{3}}\)
\(V=AA'\cdot S_{ABCD}=\dfrac{16a^3}{\sqrt{3}}\)