Cho tam giác nhọn ABC nội tiếp đường tròn và có trực tâm H.Ba điểm D, E, F lần lượt là chân các đường cao vẽ từ A, B, C của tam giác ABC. Gọi I là trung điểm của cạnh BC, P là giao điểm của EF và BC. Đường thẳng DF cắt đường tròn ngoại tiếp tam giác HEF tại điểm thứ hai là K. Đường thẳng PH cắt đường tròn ngoại tiếp tam giác HEF tại điểm thứ hai là Q. Chứng minh tứ giác BIQF nội tiếp đường tròn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M N D E
Ta có ^MEN = ^NBD + ^MCD = 1800 - ^MAN. Suy ra tứ giác AMEN nội tiếp
Cũng dễ có tứ giác BCMN nội tiếp đường tròn (BC)
Từ đó ^AEM = ^ANM = ^MCB = ^MCD = 1800 - ^MED. Hay ^AEM + ^MED = 1800
Vậy thì A,E,D thẳng hàng (đpcm).

Ta có ^BCN = ^BMN ( do tứ giác BNMC nội tiếp )
=> ^NBC = ^AMN ( cùng phụ với hai góc bằng nhau ) (1)
Mặt khác do BDEN và CDEM là các tứ giác nội tiếp chung cạnh DE
Nên ^NBD + ^MCD = ^NEM ( tính chất góc ngoài tứ giác nội tiếp )
Mà ^NBD + ^MCD + ^NAM = 1800
Suy ra ^NEM + ^NAM = 1800 . Vây AMEN nội tiếp
Do đó: ^AMN = ^AEN (2)
Từ (1) và (2) suy ra ^NBD = ^AEN
Mà ^NBD + ^DEN = 1800 (do BDEN nội tiếp)
Nên ^DEN + ^AEN = 1800 => ^AED=1800 .
Vậy ba điểm A, E, D thẳng hàng (đpcm)


a) Tứ giác BCEF có \(\widehat{BEC}=\widehat{BFC}=90^0\left(gt\right)\)
\(\Rightarrow BCEF\)là tứ giác nội tiếp.
\(\Rightarrow\widehat{C_1}=\widehat{E_1}\)
\(\Delta PBE\)và \(\Delta PFC\)có: \(\widehat{EPC}\)chung; \(\widehat{E_1}=\widehat{C_1}\)
\(\Rightarrow\Delta PBE\)![]() \(\Delta PFC\)(g.g)
\(\Delta PFC\)(g.g)
\(\Rightarrow\frac{PB}{PF}=\frac{PE}{PC}\Rightarrow PB.PC=PE.PF\)
Tứ giác BDHF có \(\widehat{BDH}=\widehat{BFH}=90^0\)(gt)
\(\widehat{BDH}+\widehat{BFH}=180^0\)
\(\Rightarrow\)BDHF là tứ giác nội tiếp.
\(\Rightarrow\widehat{B_1}=\widehat{F_1}\)
Gọi J là trung điểm của AH. Dễ thấy \(\Delta HEF\)nội tiếp đường tròn \(\left(J;\frac{AH}{2}\right)\)
Tứ giác HEKF nội tiếp đường tròn (J)
\(\Rightarrow\widehat{F_1}=\widehat{HEK}\left(=180^0-\widehat{HFK}\right)\)
Mà \(\widehat{B_1}=\widehat{F_1}\Rightarrow\widehat{B_1}=\widehat{HEK}\)
\(\Rightarrow KE//BC\left(đpcm\right)\)
b) Tứ giác BCEF nội tiếp\(\Rightarrow\widehat{B_1}=\widehat{HFE}\)
Mà \(\widehat{B_1}=\widehat{F_1}\Rightarrow\widehat{DFE}=2\widehat{B_1}\)(1)
\(\Delta EBC\)vuông tại E, đường trung tuyến EI
\(\Rightarrow IB=IE=\frac{1}{2}BC\Rightarrow\Delta IBE\)cân tại I
\(\Rightarrow\widehat{I_1}=2\widehat{B_1}\)(t/c góc ngoài của tam giác) (2)
Từ (1) và (2) suy ra \(\Rightarrow\widehat{I_1}=\widehat{DFE}\)
\(\Rightarrow DIEF\)là tứ giác nội tiếp.
Dễ chứng minh được \(\Delta PDF\)![]() \(\Delta PEI\left(g.g\right)\)
\(\Delta PEI\left(g.g\right)\)
\(\Rightarrow PD.PI=PE.PF\)
và \(\Delta PHE\)![]() \(\Delta PFQ\left(g.g\right)\)
\(\Delta PFQ\left(g.g\right)\)
\(\Rightarrow PE.PF=PH.PQ\)
\(\Rightarrow PD.PI=PH.PQ\Rightarrow\frac{PD}{PQ}=\frac{PH}{PI}\)
\(\Rightarrow\Delta PDH\)![]() \(\Delta PQI\)(c.g.c)\(\Rightarrow\widehat{PHD}=\widehat{PIQ}\)
\(\Delta PQI\)(c.g.c)\(\Rightarrow\widehat{PHD}=\widehat{PIQ}\)
Lại có \(\widehat{PHD}=\widehat{AHQ}=\widehat{AFQ}\)
\(\Rightarrow BIOF\)là tứ giác nội tiếp.

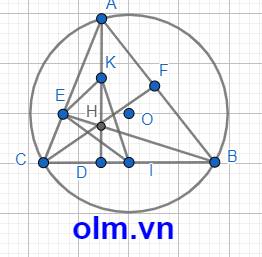
a, Xét tam giác vuông EBC vuông tại E và CI = IB
⇒ IE = IC = IB (1) ( vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)
Xét tam giác vuông BCF vuông tại F và IC =IB
⇒IF = IC = IB (2) (vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)
Từ (1) và (2) ta có:
IE = IF = IB = IC
Vậy bốn điểm B, C, E, F cùng thuộc một đường tròn tâm I bán kính bằng \(\dfrac{1}{2}\) BC (đpcm)
b, Xét \(\Delta\)AFC và \(\Delta\)AEB có:
\(\widehat{CAF}\) chung ; \(\widehat{AFC}\) = \(\widehat{AEB}\) = 900
⇒ \(\Delta\)AFC \(\sim\) \(\Delta\)AEB (g-g)
⇒ \(\dfrac{AF}{AE}\) = \(\dfrac{AC}{AB}\) (theo định nghĩa hai tam giác đồng dạng)
⇒AB.AF = AC.AE (đpcm)
Xét tam giác vuông AEH vuông tại E và KA = KH
⇒ KE = KH ( vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)
⇒\(\Delta\)EKH cân tại K ⇒ \(\widehat{KEH}\) = \(\widehat{EHK}\)
\(\widehat{EHK}\) = \(\widehat{DHB}\) (vì hai góc đối đỉnh)
⇒ \(\widehat{KEH}\) = \(\widehat{DHB}\) ( tc bắc cầu) (3)
Theo (1) ta có: IE = IB ⇒ \(\Delta\) IEB cân tại I
⇒ \(\widehat{IEB}\) = \(\widehat{IBE}\) (4)
Cộng vế với vế của (3) và(4)
Ta có: \(\widehat{KEI}\) = \(\widehat{KEH}\) + \(\widehat{IEB}\) = \(\widehat{DHB}\) + \(\widehat{IBE}\) = \(\widehat{DHB}\) + \(\widehat{DBH}\)
Vì tam giác DHB vuông tại D nên \(\widehat{DHB}\) + \(\widehat{DBH}\) = 1800 - 900 = 900
⇒\(\widehat{KEI}\) = 900
IE \(\perp\) KE (đpcm)
