Giúp mình với mn TvT
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,\) Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
\(\Rightarrow\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot d}=\dfrac{b^2}{d^2}\\ \dfrac{a^2-b^2}{c^2-d^2}=\dfrac{b^2k^2-b^2}{d^2k^2-d^2}=\dfrac{b^2\left(k^2-1\right)}{d^2\left(k^2-1\right)}=\dfrac{b^2}{d^2}\\ \Rightarrow\dfrac{ab}{cd}=\dfrac{a^2-b^2}{c^2-d^2}\)
b, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
\(\Rightarrow\left(\dfrac{a-b}{c-d}\right)^4=\left(\dfrac{bk-b}{dk-d}\right)^4=\left(\dfrac{b\left(k-1\right)}{d\left(k-1\right)}\right)^4=\dfrac{b^4}{d^4}\\ \dfrac{a^4+b^4}{c^4+d^4}=\dfrac{b^4k^4+b^4}{d^4k^4+d^4}=\dfrac{b^4\left(k^4+1\right)}{d^4\left(k^4+1\right)}=\dfrac{b^4}{d^4}\\ \RightarrowĐpcm\)
c, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
\(\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot d}=\dfrac{b^2}{d^2}\\ \dfrac{\left(a+b\right)^2}{\left(c+d\right)^2}=\dfrac{\left(bk+b\right)^2}{\left(dk+d\right)^2}=\dfrac{\left[b\left(k+1\right)\right]^2}{\left[d\left(k+1\right)\right]^2}=\dfrac{b^2\left(k+1\right)^2}{d^2\left(k+1\right)^2}=\dfrac{b^2}{d^2}\\ \RightarrowĐpcm\)


uses crt;
var s:real;
a,i,n:integer;
begin
clrscr;
readln(a,n);
s:=1;
for i:=1 to n do
if i mod 2=0 then s:=s*(a+i);
writeln(s:0:0);
readln;
end.

Số số hạng
\(\left(x-1\right):1+1=x\)
Tổng
\(\left(x+1\right)\cdot x:2=500500\) \(\left(x\ge0\right)\)
\(\left(x+1\right)x=500500\cdot2\)
\(x^2+x=1001000\)
\(x^2+x-1001000=0\)
\(\orbr{\begin{cases}x=1000\left(n\right)\\x=-1001\left(l\right)\end{cases}}\)
\(x=1000\)
Ta có: \(1+2+3+...+x=500500\)
\(\Leftrightarrow\frac{x\left(x+1\right)}{2}=500500\)
\(\Leftrightarrow x^2+x-1001000=0\)
\(\Leftrightarrow\left(x-1000\right)\left(x+1001\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=1000\left(tm\right)\\x=-1001\left(ktm\right)\end{cases}}\)

a) Điện trở tương đương của đoạn mạch :
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{60.40}{60+40}=24\left(\Omega\right)\)
b) Hiệu điện thế giữa hai đầu đoạn mạch :
\(U=I.R_{tđ}=2.24=48\left(V\right)\)
⇒ \(U=U_1=U_2=48\left(V\right)\) (vì R1 // R2)
Cường độ dòng điện chạy qua mỗi điện trở :
\(I_1=\dfrac{U_1}{R_1}=\dfrac{48}{60}=0,8\left(A\right)\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{48}{40}=1,2\left(A\right)\)
Chúc bạn học tốt





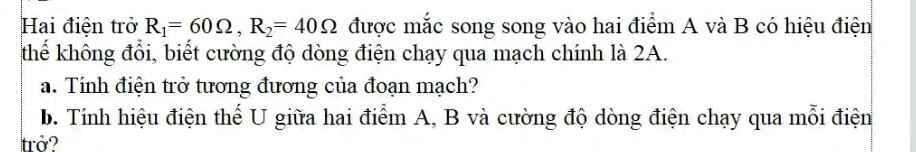
 Giúp mình với TvT
Giúp mình với TvT
a: Xét ΔDHE vuông tại H và ΔDKF vuông tại K có
DE=DF
\(\widehat{D}\) chung
Do đó: ΔDHE=ΔDKF
Suy ra: DH=DK
hay ΔDKH cân tại D