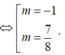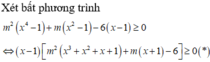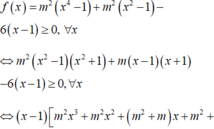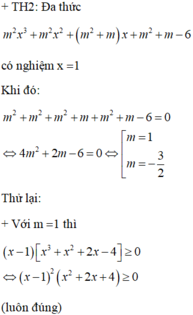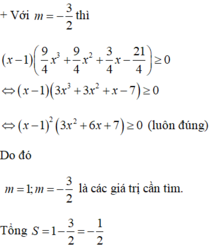Gọi S là tập hợp tất cả các giá trị của tham số m sao cho bất phương trình m2(x4 - 1) + m(x3 + 3 - 2√(x2 + 3)) - 2 (x-1) >0 đúng với mọi x ∈ R. Tính tổng giá trị của các phần tử của S
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$f(x)=m^2(x^4-1)+m(x^2-1)-6(x-1)=(x-1)[m^2(x+1)(x^2+1)+m(x+1)-6]$
Để $f(x)\geq 0$ với mọi $x\in\mathbb{R}$ thì:
$m^2(x+1)(x^2+1)+m(x+1)-6=Q(x)(x-1)^k$ với $k$ là số lẻ
$\Rightarrow h(x)=m^2(x+1)(x^2+1)+m(x+1)-6\vdots x-1$
$\Rightarrow h(1)=0$
$\Leftrightarrow 4m^2+2m-6=0$
$\Leftrightarrow 2m^2+m-3=0$
$\Leftrightarrow (m-1)(2m+3)=0\Rightarrow m=1$ hoặc $m=\frac{-3}{2}$
Thay các giá trị trên vào $f(x)$ ban đầu thì $m\in \left\{1; \frac{-3}{2}\right\}$
Tổng các giá trị của các phần tử thuộc $S$: $1+\frac{-3}{2}=\frac{-1}{2}$

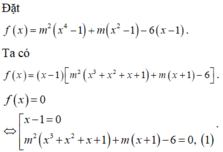
Nhận xét: Nếu x = 1 không là nghiệm của phương trình (1) thì x = 1 là nghiệm đơn của phương trình f(x) = 0 nên f(x) đổi dấu khi qua nghiệm x = 1.


Chọn C