Tìm nghiệm nguyên của phương trình: 5x2+y2=17 - 2xy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NS
1
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 9 2021
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(4x^2-4x+1\right)+\left(y^2-2y+1\right)< 3\)
\(\Leftrightarrow\left(x-y\right)^2+\left(2x-1\right)^2+\left(y-1\right)^2< 3\)
\(\Rightarrow\left(2x-1\right)^2< 3\) (1)
\(\Rightarrow\left(2x-1\right)^2=\left\{0;1\right\}\)
\(\Rightarrow\left[{}\begin{matrix}2x-1=0\\2x-1=1\\2x-1=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
- Với \(x=0\Rightarrow2y^2-2y< 1\Rightarrow\left(2y-1\right)^2< 3\Rightarrow\left[{}\begin{matrix}y=0\\y=1\end{matrix}\right.\) (giải như (1))
- Với \(x=1\Rightarrow2y^2+5< 4y+5\Rightarrow y^2-2y< 0\)
\(\Rightarrow y\left(y-2\right)< 0\Rightarrow0< y< 2\Rightarrow y=1\)
Vậy \(\left(x;y\right)=\left(0;0\right);\left(0;1\right);\left(1;1\right)\)
NS
0
AH
Akai Haruma
Giáo viên
30 tháng 11 2021
Lời giải:
$x^2-2y^2=5\Rightarrow x$ lẻ. Đặt $x=2k+1$ với $k$ nguyên
$x^2-2y^2=5$
$\Leftrightarrow (2k+1)^2-2y^2=5$
$\Leftrightarrow 2k^2+2k-y^2=2$
$\Rightarrow y$ chẵn. Đặt $y=2t$ với $t$ nguyên
PT trở thành: $2k^2+2k-4t^2=2$
$\Leftrightarrow k^2+k-2t^2=1$
Điều này vô lý do $k^2+k-2t^2=k(k+1)-2t^2$ chẵn còn $1$ thì lẻ
Vậy pt vô nghiệm.
FS
0
CM
14 tháng 4 2018
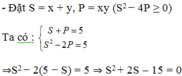
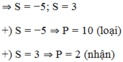
Khi đó: x, y là nghiệm của phương trình X 2 - 3 X + 2 = 0 ⇔ X = 1 ; X = 2
Vậy hệ có nghiệm (2; 1), (1; 2)
Đáp án cần chọn là: C
C
1
AH
Akai Haruma
Giáo viên
12 tháng 2 2022
Lời giải:
$x^2-2xy+5y^2=y+1$
$\Leftrightarrow x^2-2xy+y^2=y+1-4y^2$
$\Leftrightarrow y+1-4y^2=(x-y)^2\geq 0$
$\Leftrightarrow y+1-4y^2\geq 0$
$\Leftrightarrow 4y^2-y-1\leq 0$
$\Leftrightarrow 4y^2-y-3\leq -2<0$
$\Leftrightarrow (y-1)(4y+3)<0$
$\Leftrightarrow \frac{-3}{4}< y< 1$
$y$ nguyên nên $y=0$
Khi đó: $x^2=1\Leftrightarrow x=\pm 1$
Vậy $(x,y)=(\pm 1,0)$
TL
0
HL
2
7 tháng 6 2017
\(2xy-4x+y-9=0\)
\(\Leftrightarrow2x\left(y-2\right)+\left(y-2\right)-7=0\)
\(\Leftrightarrow\left(2x+1\right)\left(y-2\right)=7\)
\(\Rightarrow2x+1\) và \(y-2\) là ước của 7
đến đây dễ rồi tự làm nha
\(5x^2+y^2=17-2xy\)
Phương trình tương đương với: \(\left(x-y\right)^2+4x^2=17\Rightarrow x^2\le\frac{17}{4}\)
\(\Rightarrow x^2\in\left\{0;1;4\right\}\)
\(+)x^2=0\Rightarrow\left(x-y\right)^2=17\left(ktm\right)\)
\(+)x^2=1\Rightarrow\left(x-y\right)^2=13\left(ktm\right)\)
\(+)x^2=4\Rightarrow\left(x-y\right)^2=1\left(tm\right)\)
Với: \(x=2\Rightarrow\left(2-y\right)^2=1\Rightarrow\left[{}\begin{matrix}y=1\\y=3\end{matrix}\right.\)
Với: \(x=-2\Rightarrow\left(-2-y\right)^2=1\Rightarrow\left[{}\begin{matrix}y=-1\\y=-3\end{matrix}\right.\)
Vậy pt có 4 nghiệm: \(\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.;\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.;\left\{{}\begin{matrix}x=-2\\y=-1\end{matrix}\right.;\left\{{}\begin{matrix}x=-2\\y=-3\end{matrix}\right.\)