Biet bc=36,ac=30,ab=18.Tinh bd,cd,fa
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
3 tháng 2 2020
+ Xét \(\Delta ABC\)có :
\(AD\)là đường phân giác giác của \(\widehat{A}\)(gt)
\(\Rightarrow\frac{BD}{AB}=\frac{CD}{AC}\)( tính chất đường phân giác của tam giác )
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{BD}{AB}=\frac{CD}{AC}=\frac{BD+CD}{AB+AC}=\frac{BC}{AB+AC}=\frac{36}{18+30}=\frac{36}{48}=\frac{3}{4}\)
\(\Rightarrow\hept{\begin{cases}\frac{BD}{AB}=\frac{3}{4}\Rightarrow\frac{BD}{18}=\frac{3}{4}\Rightarrow BD=\frac{3}{4}.18=13,5\left(cm\right)\\\frac{CD}{AC}=\frac{3}{4}\Rightarrow\frac{CD}{30}=\frac{3}{4}\Rightarrow CD=\frac{3}{4}.30=22,5\left(cm\right)\end{cases}}\)
+ Xét \(\Delta ABC\)có :
\(CF\)là đường phân giác của \(\widehat{C}\)(gt)
\(\Rightarrow\frac{FA}{AC}=\frac{FB}{BC}\)( tính chất đường phân giác của tam giác )
Áp dụng tihs chất của dãy tỉ số bằng nhau ta có :
\(\frac{FA}{AC}=\frac{FB}{BC}=\frac{FA+FB}{AC+BC}=\frac{AB}{AC+BC}=\frac{18}{30+36}=\frac{18}{66}=\frac{3}{11}\)
\(\Rightarrow\frac{FA}{AC}=\frac{3}{11}\)
\(\Rightarrow\frac{FA}{30}=\frac{3}{11}\)
\(\Rightarrow FA=\frac{3}{11}.30\)
\(\Rightarrow FA\approx8,18\left(cm\right)\)
Vậy \(BD=13,5\left(cm\right);CD=22,5\left(cm\right);FA\approx8,18\left(cm\right)\)
Chúc bạn học tốt !!!
D
1
VM
31 tháng 1 2020
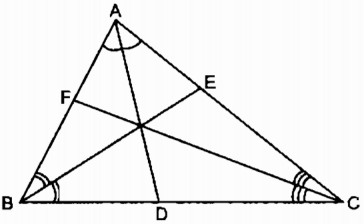
+ Xét \(\Delta ABC\) có:
\(AD\) là đường phân giác của \(\widehat{A}\left(gt\right)\)
=> \(\frac{BD}{AB}=\frac{CD}{AC}\) (tính chất đường phân giác của tam giác).
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{BD}{AB}=\frac{CD}{AC}=\frac{BD+CD}{AB+AC}=\frac{BC}{AB+AC}=\frac{36}{18+30}=\frac{36}{48}=\frac{3}{4}.\)
\(\Rightarrow\left\{{}\begin{matrix}\frac{BD}{AB}=\frac{3}{4}\Rightarrow\frac{BD}{18}=\frac{3}{4}\Rightarrow BD=\frac{3}{4}.18=13,5\left(cm\right)\\\frac{CD}{AC}=\frac{3}{4}\Rightarrow\frac{CD}{30}=\frac{3}{4}\Rightarrow CD=\frac{3}{4}.30=22,5\left(cm\right)\end{matrix}\right.\)
+ Xét \(\Delta ABC\) có:
\(CF\) là đường phân giác của \(\widehat{C}\left(gt\right)\)
=> \(\frac{FA}{AC}=\frac{FB}{BC}\) (tính chất đường phân giác của tam giác).
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{FA}{AC}=\frac{FB}{BC}=\frac{FA+FB}{AC+BC}=\frac{AB}{AC+BC}=\frac{18}{30+36}=\frac{18}{66}=\frac{3}{11}.\)
\(\Rightarrow\frac{FA}{AC}=\frac{3}{11}\)
\(\Rightarrow\frac{FA}{30}=\frac{3}{11}\)
\(\Rightarrow FA=\frac{3}{11}.30\)
\(\Rightarrow FA\approx8,18\left(cm\right).\)
Vậy \(BD=13,5\left(cm\right);CD=22,5\left(cm\right);FA\approx8,18\left(cm\right).\)
Chúc bạn học tốt!
22 tháng 1 2022
Xét tam giác ABC có: AD là phân giác (gt).
\(\Rightarrow\) \(\dfrac{DB}{DC}=\dfrac{AB}{AC}\) (Tính chất đường phân giác).
\(\Rightarrow\dfrac{DB}{DC+DB}=\dfrac{AB}{AC+AB}.\)
\(\Rightarrow\dfrac{DB}{BC}=\dfrac{AB}{AC+AB}.\)
\(Thay:\) \(\dfrac{DB}{36}=\dfrac{18}{30+18}.\Leftrightarrow DB=13,5.\)
\(DC=BC-DB=36-13,5=22,5.\)
Xét tam giác ABC có: BE là phân giác (gt).
\(\Rightarrow\) \(\dfrac{EA}{EC}=\dfrac{AB}{BC}\) (Tính chất đường phân giác).
\(\Rightarrow\) \(\dfrac{EA}{EC+EA}=\dfrac{AB}{BC+AB}.\)
\(\Rightarrow\dfrac{EA}{AC}=\dfrac{AB}{BC+AB}.\)
\(Thay:\) \(\dfrac{EA}{30}=\dfrac{18}{36+18}\Leftrightarrow EA=10.\)
\(\Rightarrow EC=AC-EA=30-10=20.\)
Xét tam giác ABC có: CF là phân giác (gt).
\(\Rightarrow\) \(\dfrac{FA}{FB}=\dfrac{AB}{BC}\) (Tính chất đường phân giác).
\(\Rightarrow\) \(\dfrac{FA}{FB+FA}=\dfrac{AB}{BC+AB}.\)
\(\Rightarrow\) \(\dfrac{FA}{AB}=\dfrac{AB}{BC+AB}.\)
\(Thay:\) \(\dfrac{FA}{18}=\dfrac{18}{36+18}\Leftrightarrow FA=6.\)
\(\Rightarrow\) \(FB=AB-FA=18-6=12.\)
18 tháng 8 2015
+) Hình thang ABCD có M;N là trung điểm của AD; BC => MN là đường trung bình của hình thang
=> MN // AB//CD và MN = (AB + CD) /2 = 10 cm
+) Xét tam giác ABD có: M là trung điểm của AD; MI // AB
=> I là trung điểm của DB
=> MI là đường trung bình của tam giác ABD => MI = AB?2 = 6/2 = 3cm
+) Xét tam giác CAB có: N là trung điểm của BC; NK //AB => K là trung điểm của AC
=> NK là đường trung bình của tam giác ABC
=> NK = AB / 2 = 6/2 = 3 cm
+) MN = MI + IK + KN = 3 + IK + 3 = 6 + IK = 10 => IK = 4 cm
24 tháng 1 2017
Bài 1:
Giải:
Xét \(\Delta ABC\left(\widehat{B}=90^o\right)\), áp dụng định lí Py-ta-go có:
\(AB^2+BC^2=AC^2\)
\(\Rightarrow10^2+5^2=AC^2\)
\(\Rightarrow AC^2=125\)
\(\Rightarrow AC=\sqrt{125}\left(dm\right)\)
Vậy \(AC=\sqrt{125}\left(dm\right)\)
Bài 2: sai đề
24 tháng 1 2017
Ta có : OB = OD = \(\frac{BD}{2}=\frac{16}{2}=8\) ( 0 là trung điểm của BD )
OA = OC = \(\frac{AC}{2}=\frac{12}{2}=6\) ( O là trung điểm của AC )
+ \(\Delta AOB\) , có :
AB2 = OA2 + OB2
AB2 = 6 + 8
AB2 = 14
AB = \(\sqrt{14}\)
Ta có : BC = CD = AD = AB
=> BC = CD = AD = AB = \(\sqrt{14}\)
thêm dữ kiện đi bạn
mk gửi đầy đủ câu mới rồi
xem câu mới nhất ý