Một ô tô đang chuyển động thẳng đều với tốc độ 72 km/h thì đột ngột
hãm phanh sau khi đi được thêm 200m thì xe dừng lại. Coi chuyển động của xe
là c/đ chậm dần đều
a) Tính gia tốc của xe
c) Sau bao lâu từ lúc hãm phanh xe còn lại vận tốc 18km/h.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
27 tháng 10 2017
Đáp án B
Gia tốc chuyển động của xe 
→ Quãng đường mà vật đi được trong 2 s cuối cùng:
Y
13 tháng 10 2023
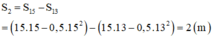
Chọn gốc tọa độ tại vị trí xe hãm phanh.
Chiều \(\left(+\right)\) là chiều chuyển động \(\left(v\ge0\right)\).
Gốc thời gian là thời điểm xe hãm phanh.
Lúc \(t=0\) thì \(v_0=72km/h=20m/s\)
\(t=10s\) thì \(v=0\)
\(a,a=?m/s^2\)
Ta có : \(a=\dfrac{\Delta v}{\Delta t}=\dfrac{v-v_0}{10}=\dfrac{0-20}{10}=-2m/s^2\)
\(b,s=?m\)
Ta có : \(d=v_0t+\dfrac{1}{2}at^2=20.10+\dfrac{1}{2}\left(-2\right).10^2=100\left(m\right)\)
Do \(v\ge0\Rightarrow s=d=100m\)
\(c,\) Quãng đường đi được của xe trong 8s đầu là :
\(s_1=v_0t_1+\dfrac{1}{2}at_1^2=20.8+\dfrac{1}{2}\left(-2\right).8^2=96\left(m\right)\)
Quãng đường đi được của xe trong 2s cuối là : \(s-s_1=100-96=4\left(m\right)\)
Vì quãng đường trong 2s đầu và 2s cuối có cùng thời gian nên ta có s của 2s đầu và cuối bằng nhau.
Vậy ...
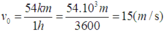
\(v_0=72\)km/h=20m/s
v=0m/s
a) Gia tốc của xe: \(v^2-v_0^2=2aS\Rightarrow0-20^2=2\cdot a\cdot200\Rightarrow a=-1\) m/s2
c) \(v'=18\) km/h=5m/s
Thời gian từ lúc hãm phanh xe còn lại vận tốc 18km/h:
\(v'=v_0+at\Rightarrow5=20-1\cdot t\Rightarrow t=15s\)