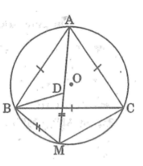
Cho tam giác nội tiếp đường trong (O) và M là một điểm trên cung nhỏ BC. Trên đoạn MA lấy điểm D sao cho MD=MB
a) Hỏi tam giác MDB là tam giác gì
b) so sánh hai tam giác BDA và BMC
c) Chứng minh MA=MB+MC
d) tìm vị trí của M để MA + MB +MC lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HD
11 tháng 2 2019
a ) Ta có BM=MD (gt)
=> \(\Delta\)MBD cân tại M
Mặt khác \(\widehat{AMB}=\widehat{ACB}\) ( Hai góc nội tiếp chắn cung AB)
Mà \(\widehat{ACB}=60^0\)( tam giác ABC đều)
Suy ra \(\widehat{AMB}=60^0hay\widehat{DMB}=60^0\)
Vậy \(\Delta MBD\) đều
b) Ta có \(\Delta MBD\) đều ( CMT)
Suy ra : \(\widehat{DMB}=\widehat{DBC}+\widehat{CBM}=60^0\)(1)
Lại có : tam giác ABC đều (gt)
Suy ra : \(\widehat{ABC}=\widehat{ABD}+\widehat{DBC}=60^0\)(2)
Từ (1) và (2) suy ra \(\widehat{ABD}=\widehat{MBC}\)
Xét hai tam giác ABD và CBM ta có
BC=BA (gt)
\(\widehat{ABD}=\widehat{MBC}\left(cmt\right)\)
BD=BM( tam giác MBD đều)
=> \(\Delta ABD=\Delta CBM\left(c.g.c\right)\)
c)\(\Delta ABD=\Delta CBM\left(cmt\right)\)
SUy ra AD=CM
mà AM=AD+DM
SUy ra MA=MC+MD
14 tháng 2 2016
bạn ơi câu a ko có dữ liệu thì tính sao được còn câu b đợi mk tí mk làm cho
14 tháng 2 2016
b) vì MD=MB ==> tam giác BDM cân tại M
mà góc BMD=góc ACB=60 độ
do đó tam giác BDM đều ==>DBM=60 độ
ta có ABD+DBC=60 độ
MBC+DBC=60 độ
==> góc ABD= CBM
DO ĐÓ TAM GIÁC ABD= tam giác CBM(c.g.c)
==> AD=CM ==> AD+DM=BM+MC=AM
==> ĐIỀU CẦN CHỨNG MINH
CM
5 tháng 3 2017
Ta có: ∆ ABD = ∆ CBM (cmt)
suy ra: AD = CM
Ta có: DM = BM ( tam giác MBD đều )
mà AM = AD + DM
suy ra: MA = MC + MB
13 tháng 2 2018
làm câu b chứ câu a chưa làm được vì đây mới lớp 8
Trên MA lấy I sao cho MI = MB. Tam giác MBI đều, suy ra \(\widehat{IBM}=60^o\)
\(\Rightarrow\)\(\widehat{B_1}=\widehat{B_2}\)
\(\Delta ABI=\Delta CBM\left(c-g-c\right)\)nên AI = MC. Từ đó MA = MB + MC.
\(\Rightarrow\)\(MA=MB+MC\left(ĐPCM\right)\)
cho mihf hỏi tam giác gì nội tiếp đường tròn O vậy
mình nghĩ đề cho bổ sung là cho tam giác ABC đều nội tiếp đường tròn ( O ) vì mình đã từng làm rồi
lời giải :
a) vì MD = MB nên \(\Delta MBD\)cân tại M
\(\widehat{BMD}=\widehat{BCA}=60^o\)( cùng chắn cung AB )
\(\Rightarrow\)\(\Delta MBD\)đều
b) Xét \(\Delta MBC\)và \(\Delta BDA\)có :
MB = BD ; BC = AB ; \(\widehat{MBC}=\widehat{DBA}\)( cùng cộng góc DBC bằng 60 độ )
\(\Rightarrow\Delta MBC=\Delta DBA\left(c.g.c\right)\)suy ra MC = AD
c) Mà MB = MD ( câu a )
nên MC + MB = MD + AD = MA
d) Ta có : MA là dây cung của ( O ; R ) \(\Rightarrow MA\le2R\)
\(\Rightarrow MB+MC+MA=2MA\le4R\)( không đổi )
Dấu " = " xảy ra \(\Leftrightarrow\)MA là đường kính hay M là điểm chính giữa của cung BC