bài 2 cho a/c= b/d cmr : (4a^2 -6ac)(4b^2 + 6bd) =(4a^2 +6ac)(4b^2 - 6bd)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cách làm như trên là không sai, tuy nhiên để chặt chẽ hơn bạn có thể làm như thế này:
Ta có:\(\left\{{}\begin{matrix}4a>4b\\-2>-3\end{matrix}\right.\), cộng 2 vế của bất phương trình ta được \(4a-2>4b-3\left(ĐPCM\right)\)

Dùng BĐT quen thuộc: \(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\) nhé! Một dòng là đủ.
\(\frac{1}{\left(4a^2+4b^2\right)}+\frac{1}{8ab}\ge\frac{4}{4a^2+8ab+4b^2}==\frac{4}{4\left(a^2+2ab+a^2\right)}=\frac{1}{\left(a+b\right)^2}^{\left(đpcm\right)}\)

\(a.2a+4b+\left(-4b+5a\right)-\left(6a-9b\right)\)
\(=2a+4b-4b+5a-6a+9b\)
\(=\left(2a+5a-6a\right)+\left(4b-4b+9b\right)\)
\(=a+9b\)
\(b.6a\left[b+3a-\left(4a-b\right)\right]\)
\(=6a\left[b+3a-4a+b\right]\)
\(=6a\left[4a-a+b+b\right]\)
\(=6a\left(3a-2b\right)\)
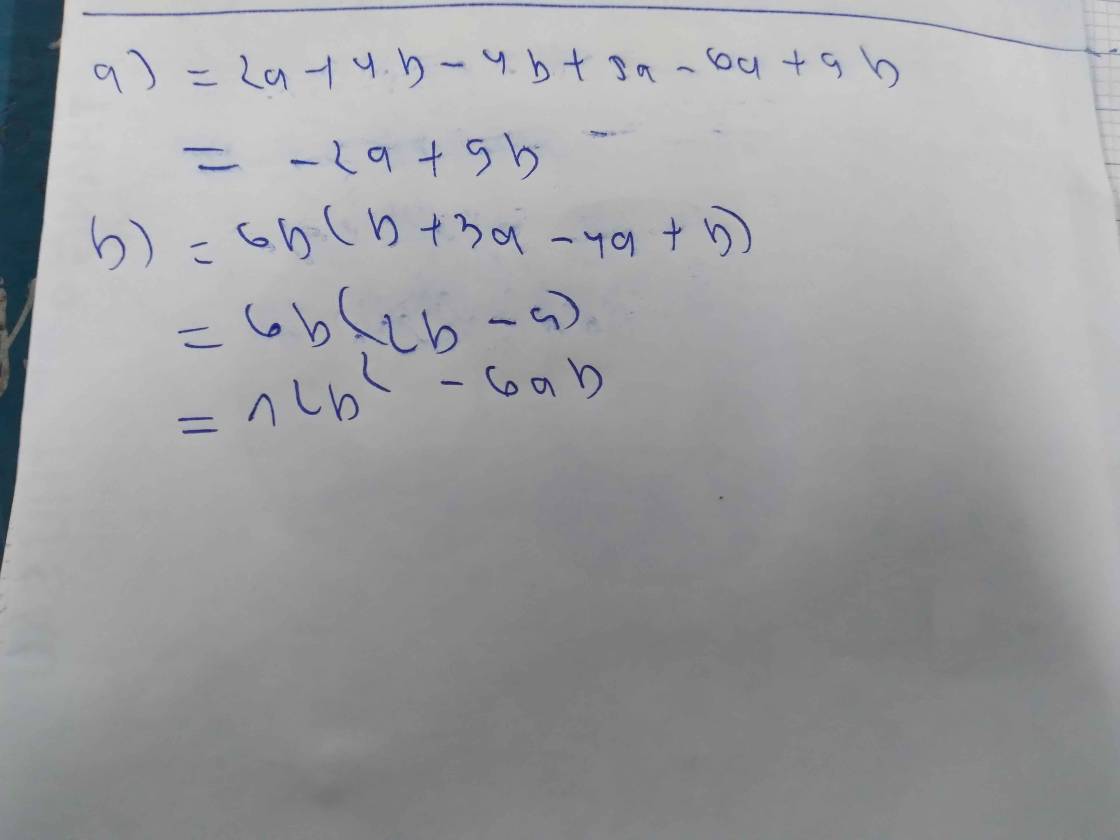
Ta có : \(\frac{a}{c}=\frac{b}{d}\Leftrightarrow\frac{a}{b}=\frac{c}{d}\)
\(\Leftrightarrow\frac{a^2}{b^2}=\frac{ac}{bd}=\frac{4a^2}{4b^2}=\frac{6ac}{6bd}=\frac{4a^2-6ac}{4b^2-6bd}=\frac{4a^2+6ac}{4b^2+6bd}\)(Áp dụng tính chất dãy tỉ số bàng nhau)
\(\Leftrightarrow\left(4a^2-6ac\right)\left(4b^2+6bd\right)=\left(4a^2+6ac\right)\left(4b^2-6bd\right)\)(Nhân chéo)
Chúc bạn học tốt!