cho tam giác ABC .từ điểm D trên cạnh BC , kẻ các đường trẳng song song với AB , AC , chúng cắt các cạnh lần lượt theo thứ tự M và N . chứng minh rằng tam giac MBD can; NDC can
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BF
25 tháng 2 2023
Tứ giác `DACM` có:
`DA` // `MC`
`DM` // `AC`
`=>` Tứ giác `DACM` là hình bình hành
`=> hat{D} = hat{C}; DA = MC`
Tương tự:
Tứ giác `AEMB` là hình bình hành có `hat{B} = hat{E}; AE = BM`
Ta có:
* `DE = DA + AE`
* `BC = BM + MC`
mà `DA = MC; AE = BM`
`=> DE = MC`
Xét tam giác `MDE` và tam giác `ACB` có:
`hat{B} = hat{E}`
` DE = MC`
`hat{D} = hat{C}`
`=>` tam giác `MDE =` tam giác `ACB` (góc - cạnh - góc)
CM
23 tháng 5 2019
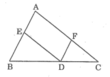
Trong tam giác ABC ta có: DE // AC (gt)
Suy ra: 
Lại có: DF // AB (gt)
Suy ra: 
Cộng từng vế (1) và (2) ta có:
CM
3 tháng 5 2019
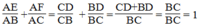
Từ N kẻ đường thẳng song song vói AB cắt BC tại K. Nối EK.
Xét ΔBEK và Δ NKE, ta có:
∠(EKB) =∠(KEN) (so le trong vì EN // BC)
EK cạnh chung
∠(BEK) =∠(NKE) (so le trong vì NK // AB))
Suy ra: Δ BEK = Δ NKE(g.c.g)
Suy ra: BE = NK (hai cạnh tương ứng)
EN = BK (hai cạnh tương ứng)
Xét Δ ADM và Δ NKC, ta có:
∠A =∠(KNC) (đồng vị vì NK // AB)
AD = NK ( vì cùng bằng BE)
∠(ADM) =∠(NKC) (vì cùng bằng góc B)
Suy ra: Δ ADM = Δ NKC(g.c.g)
Suy ra: DM = KC (hai cạnh tương ứng)
Mà BC = BK + KC. Suy ra: BC = EN + DM
6 tháng 12 2016
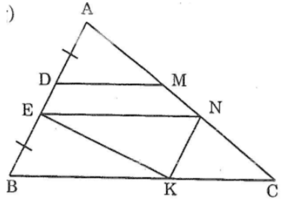
qua N kẻ đường thẳng song song với AB cắt BC tại K .
Vì EN song song với BK; NK song song với EB nên EB=NK;EN=BK (tính chất đoạn chắn)
nên NK=AD. Vì DM song song với BC nên góc( từ sau góc mình kí hiệu là >) DMA = >ACB . Vì NK song song với AB nên >A= >KNC \(\Rightarrow\) >B=>NKC Do đó ΔADM=ΔNKC (g.c.g). nên DM=KC
Suy ra DM+EN=BK+CK=BC(dpcm)
NGU LÂU GIỐT DAI KHÓ ĐÀO TẠO.
ĐÀO TẠO HẾT GẠO MÀ VẪN NGU