Trên giá sách có 4 quyển sách Toán, 3 quyển sách Văn, 2 quyển sách Ngoại ngữ.
a) Nếu chọn 2 quyển sách thì có bao nhiêu cách chọn.
b) Nếu chọn hai quyển sách khác thể loại thì có bao nhiêu cách chọn.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 7 2018
Chọn B.
TH1: 3 quyển được chọn có 2 quyển sách Văn, 1 quyển sách Toán.
Chọn 2 quyển Văn trong 6 quyển Văn khác nhau có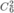 
cách.
Chọn 1 quyển Toán trong 10 quyển Toán khác nhau có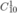 
cách.
Áp dụng quy tắc nhân, có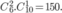 
TH2: 3 quyển được chọn có 2 quyển sách Toán, 1 quyển sách Văn.
Chọn 1 quyển Văn trong 6 quyển Văn khác nhau có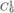 
cách.
Chọn 2 quyển Toán trong 10 quyển Toán khác nhau có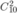 
cách.
Áp dụng quy tắc nhân, có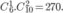 
Vậy số cách chọn ra 3 quyển sách trong đó có đúng 2 quyển cùng loại là 150 + 270 = 420.
AH
Akai Haruma
Giáo viên
24 tháng 12 2021
Lời giải:
Chọn 4 quyển sách khác nhau đủ 3 loại, có các TH sau:
TH1: 1 toán, 1 lý, 2 hóa: $A_1=C^1_6.C^1_7.C^2_8$ cách
TH2: 2 toán, 1 lý, 1 hóa: $A_2=C^2_6.C^1_7.C^1_8$ cách
TH3: 1 toán, 2 lý, 1 hóa: $A_3=C^1_6.C^2_7.C^1_8$ cách
Tổng số cách: $A_1+A_2+A_3=3024$ cách
CM
14 tháng 1 2019
Xếp theo thứ tự: ngữ văn- toán- ngữ văn- toán- ngữ văn- toán-ngữ văn-toán- ngữ văn. Vậy có 5.4.4.3.3.2.2.1=2880 cách
Chọn B
CM
18 tháng 4 2018
a) Có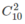 
cách chọn hai quyển từ tầng thứ k, k = 1, 2, 3, 4
Vậy có tất cả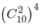 
cách chọn.
b) Tương tự, có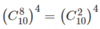 
cách chọn.
18 tháng 5 2017
a) \(C^2_{10}\) cách chọn hai quyển từ tầng \(k,k=1,2,3,4\). Vậy có tất cả \(\left(C^2_{10}\right)^4\) cách chọn
b) Tương tự, có \(\left(C^8_{10}\right)^4=\left(C^2_{10}\right)^4\) cách chọn
CM
20 tháng 2 2019
c. Số cách chọn 2 quyển sách khác môn học là: 5×6+5×8+6×8=118
Chọn C
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 4 2023
Xếp 5 quyển Toán cạnh nhau: \(5!\) cách
Xếp 5 quyển Lý cạnh nhau: \(4!\) cách
Xếp 3 quyển Văn cạnh nhau: \(3!\) cách
Hoán vị 3 loại Toán-Lý-Văn: \(3!\) cách
Tổng cộng có: \(5!.4!.3!.3!=...\) cách xếp thỏa mãn
a, Có \(C^2_9=36\) cách chọn 2 cuốn sách.
b, TH1: 1 quyển sách toán và 1 quyển sách văn.
Có 4 cách chọn sách toán.
Có 3 cách chọn sách văn.
\(\Rightarrow\) Có \(4.3=12\) cách chọn thỏa mãn.
TH2: 1 quyển sách toán và 1 quyển sách ngoại ngữ.
Có 4 cách chọn sách toán.
Có 2 cách chọn sách ngoại ngữ.
\(\Rightarrow\) Có \(4.2=8\) cách chọn thỏa mãn.
TH3: 1 quyển sách văn và 1 quyển sách ngoại ngữ.
Có 3 cách chọn sách văn.
Có 2 cách chọn sách ngoại ngữ.
\(\Rightarrow\) Có \(3.2=6\) cách chọn thỏa mãn.
Vậy có \(12+8+6=26\) cách chọn thỏa mãn yêu cầu bài toán.