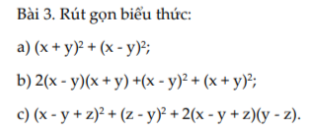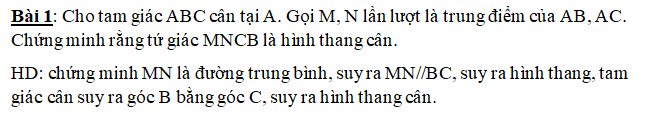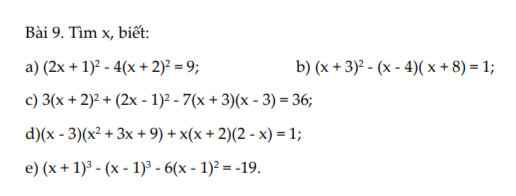ai chỉ giúp em...
Đọc tiếp
ai chỉ giúp em vs
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 10 2021
\(a,=\left(x+y+x-y\right)\left(x+y-x+y\right)=4xy\\ b,=\left(x+y+x-y\right)^2=4x^2\\ c,=\left(x-y+z\right)^2+\left(z-y\right)^2-2\left(x-y+z\right)\left(z-y\right)\\ =\left(x-y+z-z+y\right)^2=x^2\)
HM
1
3 tháng 10 2021
Xét ΔBAC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân
PL
2
DT
Đỗ Thanh Hải
CTVVIP
21 tháng 8 2021
1 has changed
2 are driving
3 were made
4 went - saw
5 finish
6 have been
7 weren't
8 will write
9 doing
10 to work
11 will clean
12 tastes - are
13 has become
14 went
15 is learning
16 won't be
17 is cut
18 eats
19 stewing
20 to drink
21 is organised
22 built
23 were made
14 was set
25 haven't done
26 is speaking
27 are spoken
3 tháng 10 2021
a) \(\left(2x+1\right)^2-4\left(x+2\right)^2=9\\ \Rightarrow\left(2x+1\right)^2-\left[2\left(x+2\right)\right]^2=9\\ \Rightarrow\left(2x+1-2x-4\right)\left(2x+1+2x+4\right)=9\\ \Rightarrow-3\left(4x+5\right)=9\\ \Rightarrow-12x-15=9\\ \Rightarrow x=-2\)
b) \(\left(x+3\right)^2-\left(x-4\right)\left(x+8\right)=1\\ \Rightarrow x^2+6x+9-\left(x^2+4x-32\right)=1\\ \Rightarrow x^2+6x+9-x^2-4x+32=1\\ \Rightarrow2x=-40\\ \Rightarrow x=-20\)
3 tháng 10 2021
\(a,\Rightarrow4x^2+4x+1-4x^2-16x-16=9\\ \Rightarrow-12x=24\Rightarrow x=-2\\ b,\Rightarrow x^2+6x+9-x^2-4x+32=1\\ \Rightarrow2x=-40\Rightarrow x=-20\\ c,\Rightarrow3x^2+12x+12+4x^2-4x+1-7x^2+63=36\\ \Rightarrow8x=-40\Rightarrow x=-5\\ d,\Rightarrow x^3-27+4x-x^3=1\\ \Rightarrow4x=28\Rightarrow x=7\\ e,\Rightarrow x^3+3x^2+3x+1-x^3+3x^2-3x+1-6x^2+12x-6=-19\\ \Rightarrow12x=-15\Rightarrow x=-\dfrac{5}{4}\)
TN
1
10 tháng 1 2022
a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.
TM
26 tháng 3 2022
15. Gọi chiều dài là x, chiều rộng là y (x, y > 0).
- 2 lần chiều dài bằng 3 lần chiều rộng \(\Rightarrow2x=3y\left(1\right)\)
- Nửa chu vi bằng 20 (cm) \(\Rightarrow x+y=20\left(2\right)\)
Từ (1) và (2), ta có hệ phương trình : \(\left\{{}\begin{matrix}2x=3y\\x+y=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3y}{2}\\\dfrac{3y}{2}+y=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3y}{2}\\3y+2y=40\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3.8}{2}\\y=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=12\left(tmđk\right)\\y=8\left(tmđk\right)\end{matrix}\right.\)
Vậy : ...