Cho \(\Delta ABC\) vuông tại \(A\) ( AB < AC ) nội tiếp (O), đường kính BC . Kẻ dây \(AD\perp BC\).Gọi E là giao điểm của DB & CA . Qua E kẻ đường thẳng vuông góc BC tại H & cắt AB tại F . CMR :
a, \(\Delta EBF\) cân
b, \(\Lambda HAF\) cân
c, HA là tiếp tuyến...
Đọc tiếp
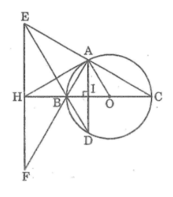
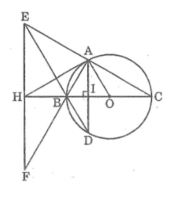
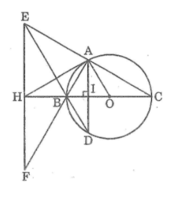
Cho \(\Delta ABC\) vuông tại \(A\) ( AB < AC ) nội tiếp (O), đường kính BC . Kẻ dây \(AD\perp BC\).Gọi E là giao điểm của DB & CA . Qua E kẻ đường thẳng vuông góc BC tại H & cắt AB tại F . CMR :
a, \(\Delta EBF\) cân
b, \(\Lambda HAF\) cân
c, HA là tiếp tuyến (O)
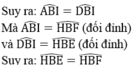
a)Ta có:AD v/góc BC =>BC là trung trực của AD(đ/lý đkính và dây cung)
=> tam giác DBA cân tại B=>BDA=DAB(t/c)
Lại có EF//AD(cùng v/góc HC)
=>BEF=BDA=BFE=DAB
=> tam giác BEF cân tại B
b)Ta có: tam giác BEF cân tại B có BH là đường cao
=> BH cũng là trung tuyến
=>HE=HF
Mặt khác:FAE=90o (kề bù với BAC)
Xét tam giác EAF vuông tại A có AH là trung tuyến
=> HA=HF=HE
=>tam giác HAF cân
c)\(\Delta\) FHB có HFB+HBF=90o (FHB=90o)(3)
Mà \(\left\{{}\begin{matrix}\text{HAF=HFA(HAF cân)(4)}\\HBF=ABO\left(đ.đ\right)\left(1\right)\end{matrix}\right.\)
Lại có:OB=OA=R
=>\(\Delta\)OBA cân tại O =>OBA=OAB(2)
Từ (1)(2)=>HBF=BAO(5)
Từ (3)(4)(5)=>HFB+HBF=BAO+HAF=90o=HAO
=>HA là tiếp tuyến của (O)(đpcm)