Bài 2. Cho tam giác ABC vuông tại A có AD là đường trung tuyến. Kẻ DH // AC và DK // AB (H thuộc AB, K thuộc AC)
a) Chứng minh H là trung điểm của AB và K là trung điểm của AC
b) Chứng minh AHDK là hình chữ nhật
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABD và ΔACD có
AB=AC
AD chung
BD=CD
Do đó: ΔABD=ΔACD

a: Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{HAK}=90^0\)
=>AHMK là hình chữ nhật
=>AM=HK
b: Xét ΔABC có
M là trung điểm của BC
MK//AB
Do đó: K là trung điểm của AC
Xét ΔABC có
M là trung điểm của BC
MH//AC
Do đó: H là trung điểm của AB
Xét ΔABC có
M,K lần lượt là trung điểm của CB,CA
=>MK là đường trung bình của ΔABC
=>MK//AB và \(MK=\dfrac{AB}{2}\)
Ta có: MK//AB
H\(\in\)AB
Do đó: MK//HB
Ta có: \(MK=\dfrac{AB}{2}\)
\(AH=HB=\dfrac{AB}{2}\)
Do đó: MK=AH=HB
Xét tứ giác BHKM có
BH//KM
BH=KM
Do đó: BHKM là hình bình hành
c: Gọi O là giao điểm của AM và KH
Ta có: AHMK là hình chữ nhật
=>AM cắt KH tại trung điểm của mỗi đường
=>O là trung điểm của AM và KH
=>\(OA=OM=\dfrac{AM}{2};OK=OH=\dfrac{KH}{2}\)
mà AM=KH
nên OA=OM=OK=OH(1)
Xét ΔAKM có
AF,KO là các đường trung tuyến
AF cắt KO tại D
Do đó: D là trọng tâm của ΔAKM
Xét ΔAKM có
D là trọng tâm
KO là đường trung tuyến
Do đó: \(KD=\dfrac{2}{3}KO\left(2\right)\)
Xét ΔHAM có
AE,HO là các đường trung tuyến
AE cắt HO tại I
Do đó: I là trọng tâm của ΔHAM
Xét ΔHAM có
HO là đường trung tuyến
I là trọng tâm
Do đó: \(HI=\dfrac{2}{3}HO\left(3\right)\)
Từ (1),(2),(3) suy ra HI=KD
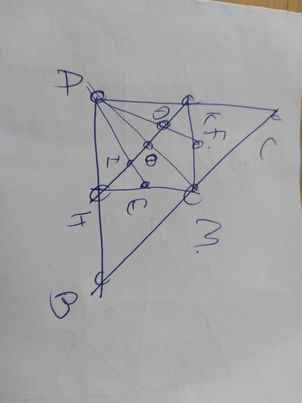

a) Xét tam giác ADH vuông tại H và tam giác ADK vuông tại K
có: góc DAH = góc DAK (gt)
AD là cạnh chung
\(\Rightarrow\Delta ADH=\Delta ADK\left(ch-gn\right)\)
=> DH = DK ( 2 cạnh tương ứng)
b) Xét tam giác HDM vuông tại H và tam giác KDN vuông tại K
có: HD = KD ( phần a)
góc HDM = góc KDN ( đối đỉnh)
\(\Rightarrow\Delta HDM=\Delta KDN\left(cgv-gn\right)\)
=> DM = DN ( 2 cạnh tương ứng)
=> tam giác DMN cân tại D ( định lí tam giác cân)
c) Xét tam giác DMN
có: MI = NI
=> DI là đường trung tuyến của MN ( định lí đường trung tuyến) (*)
ta có: tam giác ADH = tam giác ADK ( chứng minh phần a)
=> AH = AK ( 2 cạnh tương ứng) (1)
ta có: tam giác HDM = tam giác KDN ( chứng minh phần b)
=> HM = KN ( 2 cạnh tương ứng) (2)
Từ (1);(2) => AH + HM = AK + KN
=> AM = AN
=> tam giác AMN cân tại A ( định lí tam giác cân)
mà AD là đường phân giác của góc A (gt)
=> AD là đường trung tuyến của MN ( định lí) (**)
Từ(*);(**) => A,D,I thẳng hàng
mk ko bít kẻ hình đâu! Bn kẻ hình hộ mk nhé! thanks

a: Xét ΔABC có
D là trung điểm của BC
DH//AC
Do đó: H là trung điểm của AB
Xét ΔBAC có
D là trung điểm của BC
DK//AB
Do đó: K là trung điểm của AC
b: Xét tứ giác AKDH có
DH//AK
DK//AH
Do đó: AKDH là hình bình hành
mà \(\widehat{KAH}=90^0\)
nên AKDH là hình chữ nhật

4 bài toàn là hình, lại khó, dài , mk nghĩ chắc ko ai tl giúp bn đâu, xl nha, ngay mk mới lp 6 cx chưa thể giải đc vì đã lp 7 đâu. ah hay là bn gửi tg bài 1 cho các bn ấy giải từ từ, cứ 1 đốg thì ai giải giúp bn đc. sorry nha
*In đậm: quan trọng.
a: Xét ΔABC có
D là trung điểm của BC
DH//AC
Do đó: H là trung điểm của AB
Xét ΔABC có
D là trung điểm của BC
DK//AB
Do đó: K là trung điểm của AC