ai giải hộ mik bài này với lớp 8 nha
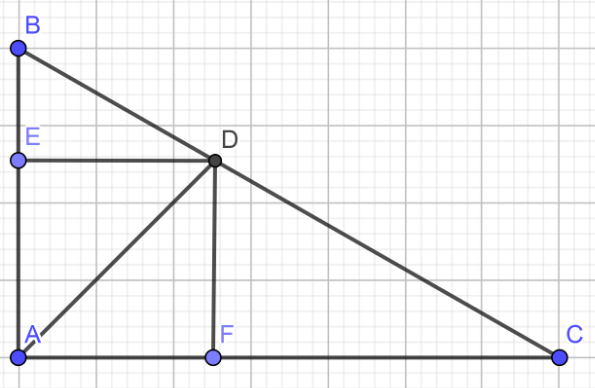
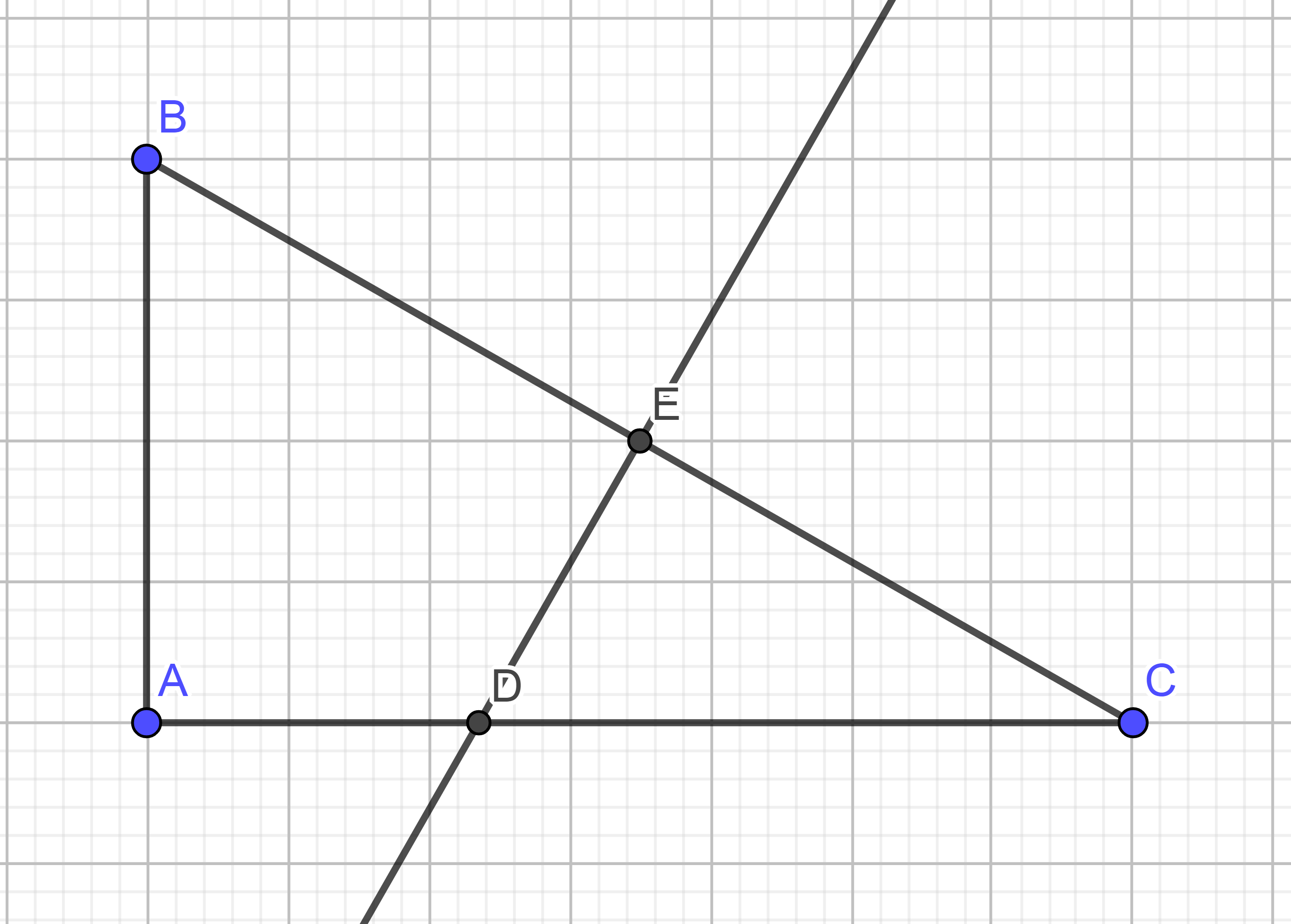
Cho tam giác ABC vuông tại A(AB<AC) có phân giác AD, đường cao AH và trung tuyến AM. Gọi E và F là chân đường vuông góc hạ từ D xuống AB và AC. a) Chứng minh tứ giác AEDF là hình vuông b) chứng minh AD là phân giác của góc MAH.