chứng mnh biểu thức luân âm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=x^2-4x+7=x^2-4x+4+3=\left(x-2\right)^2+3\ge3>0\forall x\)
Vậy ta có đpcm
\(B=4x^2-12x+11=4x^2-12x+9+2=\left(2x-3\right)^2+2\ge2>0\forall x\)
Vậy ta có đpcm
\(C=x^2-x+1=x^2-x+\frac{1}{4}+\frac{3}{4}=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\forall x\)
Vậy ta có đpcm
\(\hept{\begin{cases}A=x^2-4x+4+3=\left(x-2\right)^2+3\ge3>0\\B=4x^2-12x+9+2=\left(2x-3\right)^2+2\ge2>0\\C=x^2-x+\frac{1}{4}+\frac{3}{4}=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\end{cases}}\)

\(-2x^2+3x-4=-2\left(x^2-\dfrac{3}{2}x+\dfrac{9}{16}\right)-\dfrac{23}{8}=-2\left(x-\dfrac{3}{4}\right)^2-\dfrac{23}{8}\le-\dfrac{23}{8}< 0\)

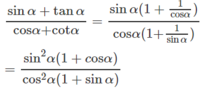
Vì 1 + cosα ≥ 0 và 1 + sinα ≥ 0 cho nên biểu thức đã cho không thể có giá trị là một số âm.


a) Ta có: 9 c 2 – 6c + 3 = ( 3 c – 1 ) 2 + 2 > 0 "m.
b) Tương tự.

Đề bài sai nhé bạn
Ví dụ x = 1 thì bthức = -1 - 6 + 10 = 3 không âm
\(-x^2-6x+10\)
\(=-1\left(x^2+6x-10\right)\)
=> -x^2-6x+10 < 0 với mọi x
a) \(A=-x^2+2x-5=-\left(x^2-2x+1\right)-4\)
\(=-\left(x-1\right)^2-4\le-4\)
\(maxA=-4\Leftrightarrow x=1\)
b) \(B=-x^2+x-1=-\left(x^2-x+\dfrac{1}{4}\right)-\dfrac{3}{4}\)
\(=-\left(x-\dfrac{1}{2}\right)^2-\dfrac{3}{4}\le-\dfrac{3}{4}\)
\(maxB=-\dfrac{3}{4}\Leftrightarrow x=\dfrac{1}{2}\)
c) \(C=-4x^2-16x-9=-\left(4x^2+16x+16\right)+7\)
\(=-\left(2x+4\right)^2+7\le7\)
\(maxC=7\Leftrightarrow x=-2\)