Một vật chuyển động có phương trình với vận tốc v = (10 – 2t) (m/s). Sau 2s kể từ thời điểm t = 0, vật đi được quãng đường bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
27 tháng 5 2019
Chọn D.
Vì t = 0 thì v0 = 10m/s > 0, tức là chiều dương của trục tọa độ được chọn cùng chiều với chuyển động của thang máy
Đối chiếu v = (10 – 2t) (m/s) với công thức v = v0 + at suy ra: v 0 = 10 ( m / s ) a = - 2 ( m / s 2 )
Vật dừng lại khi: v = (10 – 2t) = 0 => t = 5s. Từ t = 0 đến t = 5s vật chuyển động chậm dần đều với gia tốc – 2m/s2 và từ t = 5s đến t = 9s vật chuyển động nhanh dần đều với gia tốc 2m/s2.
VT
24 tháng 7 2017
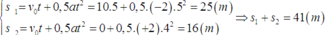
Chọn C.
Vì t = 0 thì v0 = 10m/s > 0, tức là chiều dương của trục tọa độ được chon cùng chiều với chuyển động của vật
Đối chiếu v = (10 – 2t) (m/s) với công thức v = v0 + at suy ra: v 0 = 10 ( m / s ) a = - 2 ( m / s 2 )
Từ: s = v0t + 0,5at2 = 10.4,5 + 0,5.(-2).4,52 = 24,75 (m)
VT
20 tháng 2 2019
Chọn C.
Vì t = 0 thì vo = 10 m/s > 0, tức là chiều dương của trục tọa độ được chọn cùng chiều chuyển động của thang máy này.
Đối chiếu v = (10 + 2t) (m/s) với công thức v = v0 + at suy ra: v 0 = + 10 ( m / s ) a = + 2 ( m / s 2 )
Từ: s = v 0 t + 0 , 5 a t 2 = 10 . 10 + 0 , 5 . 2 . 10 2 = 200 ( m )
Phân tích: Vì t = 0 thì v0 = 10m/s > 0, tức là chiều dương của trục tọa độ được chon cùng chiều với chuyển động của vật Đối chiếu v = (10 – 2t) (m/s) với công thức v = v0 + at suy ra: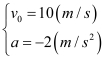
\(s=v_ot+0,5at^2=10.5+0,5.\left(-2\right).5^2=25\left(m\right)\)