cho hai số -3 và 23, xen kẽ giữa hai số đó là n số hạng để tất cả các số đó tạo thành cấp số cộng có cộng sai d=2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 12 2018
Theo giả thiết thì ta được một cấp số cộng có n+2 số hạng với u 1 = − 3 , u n + 2 = 23.
Khi đó u n + 2 = u 1 + n + 1 d ⇔ n + 1 = u n + 2 − u 1 d = 23 − − 3 2 = 13 ⇔ n = 12
Chọn đáp án A.
CM
7 tháng 4 2018
u 12 = 23 S 12 = 144 ⇒ u 1 + 11 d = 23 12 2 u 1 + u 12 = 144 ⇔ u 1 + 11 d = 23 u 1 + 23 = 24 ⇔ u 1 = 1 d = 23 − u 1 11 = 2
Chọn đáp án A
CM
7 tháng 11 2019
Chọn A
Theo giả thiết ta có: u 1 = 2 u 5 = 22
Mà u5 = u1 + 4d nên 22 = 2 + 4d
⇒ 20 = 4 d ⇔ d = 5
⇒ u 2 = 2 + 5 = 7 u 3 = 2 + 2.5 = 12 u 4 = 2 + 3.5 = 17
Vậy tổng ba số viết xen giữa là: 7 +12 +17 = 36
CM
2 tháng 4 2019
Chọn A
Nếu xen 4 số vào giữa hai số để được một cấp số cộng thì cấp số cộng đó có 6 số hạng.
Theo đầu bài
Ta có: u 1 = 4 ; u 6 = 40
⇒ 40 = 4 + 5. d ⇒ d = 7 , 2
Vậy 4 số thêm vào là:11,2; 18,4; 25,6; 32,8
NM
0
27 tháng 10 2023
Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77
CM
13 tháng 9 2019
Chọn B.
Gọi bốn số đó là a ;b ;c ;d ta có hệ:
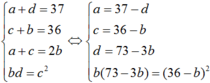
Giải ra ta được : b = 16 ; c = 20 ; d = 25 ; a = 12.