giá trị lớn nhất của (9*x2-12*x+4)/(x2-2*x+2)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(\frac{9x^2-12x+4}{x^2-2x+2}\)
= \(\frac{9\left(x^2-2x+2\right)+6x-14}{x^2-2x+2}\)
= \(9+\frac{6x-14}{x^2-2x+2}\)
= \(9+\frac{x^2-2x+2-\left(x^2-8x+16\right)}{\left(x^2-2x+1\right)+1}\)
= \(9+1-\frac{\left(x-4\right)^2}{\left(x-1\right)^2+1}\)
= \(10-\frac{\left(x-4\right)^2}{\left(x-1\right)^2+1}\le10\forall x\)
Dấu "=" xảy ra <=> x - 4 = 0 <=> x = 4
Vậy Max của \(\frac{9x^2-12x+4}{x^2-2x+2}\)= 10 khi x = 4


\(a,\\ A=25x^2-10x+11\\ =\left(5x\right)^2-2.5x.1+1^2+10\\ =\left(5x+1\right)^2+10\ge10\forall x\in R\\ Vậy:min_A=10.khi.5x+1=0\Leftrightarrow x=-\dfrac{1}{5}\\ B=\left(x-3\right)^2+\left(11-x\right)^2\\ =\left(x^2-6x+9\right)+\left(121-22x+x^2\right)\\ =x^2+x^2-6x-22x+9+121=2x^2-28x+130\\ =2\left(x^2-14x+49\right)+32\\ =2\left(x-7\right)^2+32\\ Vì:2\left(x-7\right)^2\ge0\forall x\in R\\ Nên:2\left(x-7\right)^2+32\ge32\forall x\in R\\ Vậy:min_B=32.khi.\left(x-7\right)=0\Leftrightarrow x=7\\Tương.tự.cho.biểu.thức.C\)
b:
\(D=-25x^2+10x-1-10\)
\(=-\left(25x^2-10x+1\right)-10\)
\(=-\left(5x-1\right)^2-10< =-10\)
Dấu = xảy ra khi x=1/5
\(E=-9x^2-6x-1+20\)
\(=-\left(9x^2+6x+1\right)+20\)
\(=-\left(3x+1\right)^2+20< =20\)
Dấu = xảy ra khi x=-1/3
\(F=-x^2+2x-1+1\)
\(=-\left(x^2-2x+1\right)+1=-\left(x-1\right)^2+1< =1\)
Dấu = xảy ra khi x=1

Bài 3:
a) Ta có: \(A=25x^2-20x+7\)
\(=\left(5x\right)^2-2\cdot5x\cdot2+4+3\)
\(=\left(5x-2\right)^2+3>0\forall x\)(đpcm)
d) Ta có: \(D=x^2-2x+2\)
\(=x^2-2x+1+1\)
\(=\left(x-1\right)^2+1>0\forall x\)(đpcm)
Bài 1:
a) Ta có: \(A=x^2-2x+5\)
\(=x^2-2x+1+4\)
\(=\left(x-1\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi x=1
b) Ta có: \(B=x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)

Xét trên \(\left[-1;2\right]\Rightarrow y=x^2-2x-8\) có \(-\dfrac{b}{2a}=1\)
\(y\left(-1\right)=-5;y\left(1\right)=-9;y\left(2\right)=-8\)
Xét trên \((2;4]\Rightarrow y=2x-12\)
\(y\left(4\right)=-4\)
So sánh các giá trị trên, ta được \(M=-4;m=-9\)
\(\Rightarrow M+m=-13\)
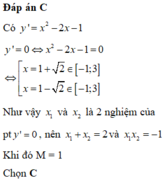
Đặt \(P=\frac{9x^2-12x+4}{x^2-2x+2}\)
\(=\frac{10\left(x^2-2x+2\right)-x^2+8x-16}{x^2-2x+2}\)
\(=\frac{10\left(x^2-2x+2\right)}{x^2-2x+2}-\frac{x^2-8x+16}{x^2-2x+2}\)
\(=10-\frac{\left(x-4\right)^2}{x^2-2x+2}\)
Ta thấy : \(\frac{\left(x-4\right)^2}{x^2-2x+2}\ge0\left(x^2-2x+2=\left(x-1\right)^2+1,\left(x-4\right)^2\ge0\right)\)
\(\Rightarrow10-\frac{\left(x-4\right)^2}{x^2-2x+2}\le10\)
hay \(P\le10\)
Dấu "=" xảy ra \(\Leftrightarrow x=4\)
Vậy : GTLN của \(P=10\Leftrightarrow x=4\)