cho nửa đường tròn tâm O đg kính AB. gọi Ax, By là các tia vuông góc với AB. Trên nửa đg tròn lấy điểm C, qua C vẽ tiếp tuyến với nửa đg tròn, nó cắt Ax, By lần lượt tại M và N. tia AC cắt By tại E
a. CM AE song song với ON
b.gọi H là hình chiếu của C trên AB, I là giao điểm của AN và BM. CMR I là trung điểm của...
Đọc tiếp
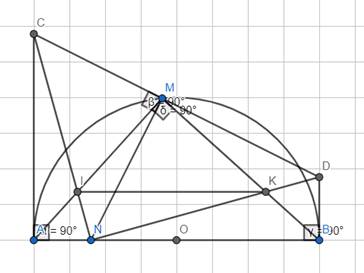
cho nửa đường tròn tâm O đg kính AB. gọi Ax, By là các tia vuông góc với AB. Trên nửa đg tròn lấy điểm C, qua C vẽ tiếp tuyến với nửa đg tròn, nó cắt Ax, By lần lượt tại M và N. tia AC cắt By tại E
a. CM AE song song với ON
b.gọi H là hình chiếu của C trên AB, I là giao điểm của AN và BM. CMR I là trung điểm của CH
a) Nối cạnh BC
Ta có :
Tam giác ABC nội tiếp (O) đường kính AB suy ra tam giác ABC vuông tại C
\(\rightarrow\) AC vuông góc với BC (1)
Mặt khác: NC và NB là 2 tiếp tuyết cắt nhau \(\rightarrow NC=NB\)
Lại có\(OC=OB,NC=NB\)
\(\rightarrow\) ON là đường trung trực BC
\(\rightarrow ON\perp BC\left(2\right)\)
Từ (1) và (2)\(\rightarrow AC//ON\) hay \(AE//ON\) (Đpcm)