Tìm các số nguyên x , y biết : \(x^2+xy-3x-3y+7 \)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NM
2
16 tháng 2 2020
a)Ta có :\(xy-2x-3y=9\)
\(x.\left(y-2\right)\)-\(3.\left(y-2\right)\)\(-6=9\)
\(\left(x-3\right)\)\(.\left(y-2\right)\)\(=15\)
đến đây cậu tự làm tiếp nhé
16 tháng 2 2020
| x-3 | 1 | 15 | -1 | -15 | 3 | 5 | -3 | -5 |
| y-2 | 15 | 1 | -15 | -1 | 5 | 3 | -5 | -3 |
| x | 4 | 18 | 2 | -12 | 6 | 8 | 0 | -2 |
| y | 17 | 3 | -13 | 1 | 7 | 5 | -3 | -1 |
DL
0
NP
1
AH
Akai Haruma
Giáo viên
23 tháng 12 2022
Lời giải:
$xy+3x+3y=-16$
$(xy+3x)+(3y+9)=-7$
$x(y+3)+3(y+3)=-7$
$(y+3)(x+3)=-7$
Vì $x,y$ nguyên nên $x+3, y+3$ nguyên. Ta có bảng sau: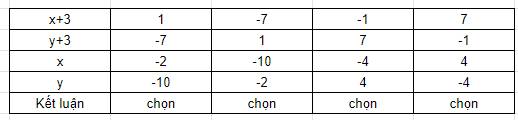
TK
3
29 tháng 12 2021
1: \(\Leftrightarrow n+3\in\left\{1;-1;19;-19\right\}\)
hay \(n\in\left\{-2;-4;16;-22\right\}\)
AH
Akai Haruma
Giáo viên
29 tháng 12 2021
1.
$4n-7\vdots n+3$
$\Rightarrow 4(n+3)-19\vdots n+3$
$\Rightarrow 19\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 19\right\}$
$\Rightarrow n\in\left\{-2; -4; 16; -22\right\}$
VM
4
4 tháng 11 2015
x^2+xy-3x-3y+7=0
=>(x-3)(x+y)+7=0
=>7=(3-x)(x+y)
=>x+y,3-x thuộc -7,-1,1,7
=>x+y=-7,3-x=-1 hoặc x+y=-1,3-x=-7 hoặc x+y=7,3-x=1 hoặc x+y=1,3-x=7.
=>(x,y) thuộc (4;-11),(10;-11),(2;5),(-4;5)
BD
23 tháng 6 2023
\(a.\left(x-3\right)\cdot\left(y+2\right)=7\)Ư(7) = {1;-1;7;-7}
\(=>x-3\inƯ\left(7\right);y+2\inƯ\left(7\right)\)
Th1 : x - 3 = 1 ; y + 2 = 7
x-3 =1
=> x =4
y + 2 =7
=> y=5
Th2 : x - 3 = 7 ; y + 2 = 1
x-3 = 7
=> x = 10
y + 2 =1
=> y = -1
Th3 : x - 3 = -1 ; y + 2 = -7
x - 3 = -1
=> x = 2
y + 2 = -7
=> y= -9
Th4 : x - 3 = -7 ; y + 2 = -1
x - 3 = -7
=> x = -4
y+2 =-1
=> y=-3
Vậy {(y=-3 ; x=-4), (y=-9;x=2);(y=-1;x=10); ( y=5 ; x =4 )}
b. xy -2y + 3x-6 = 3
y(x-2) + 3(x-2)= 3
(x-2) . (y + 3) = 3
x-2 ϵ Ư(3); y+3 ϵ Ư(3)
Ư(3) = {-1;1;-3;3)
Th1 : x -2 = -1 ; y+3 = -3
x-2 =-1 y+3=-3
=> x=1 => y=-6
Th2 : x -2 = -3 ; y+3 = -1
x-2=-3 y+3=-1
=> x= -1 => y =-4
Th3 : x -2 = 1; y+3 = 3
x-2 = 1 y+3=3
=> x=3 => y = 0
Th4 : x -2 = 3; y+3 = 1
x- 2 = 3 y +3 = 1
=> x = 5 => y = -2
Vậy {(y=-6 ; x=1), (y=-4;x=-1);(y=0;x=3); ( y=-2 ; x =5 )}
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
23 tháng 6 2023
a, (\(x\) - 3)(\(y\) + 2) = 7
Ư(7) = { -7; -1; 1; 7}
Lập bảng ta có:
| \(x-3\) | -7 | -1 | 1 | 7 |
| \(x\) | -4 | 2 | 4 | 10 |
| \(y\) + 2 | -1 | -7 | 7 | 1 |
| \(y\) | -3 | -9 | 5 | -1 |
Theo bảng trên ta có:
Các cặp giá trị \(x;y\) nguyên thỏa mãn đề bài lần lượt là:
(\(x;y\)) = (-4; -3); (2; -9); (4; 5); (10; -1)
b, \(xy\) - 2\(y\) + 3\(x\) - 6 = 3
(\(xy\) + 3\(x\)) = 3 + 2\(y\) + 6
\(x\left(y+3\right)\) = 9 + 2\(y\)
\(x\) = (9 + 2\(y\)) : (\(y\) + 3)
\(x\) \(\in\) Z ⇔ 9 + 2\(y\)⋮\(y+3\) ⇒ 2\(y\) + 6 + 3 ⋮ \(y\)\(+3\)⇒2(\(y\)+3) + 3⋮\(y\)+ 3
⇒ 3 ⋮ \(y\) + 3
Ư(3) = (-3; -1; 1; 3}
Lập bảng ta có:
| \(y\) + 3 | -3 | -1 | 1 | 3 |
| \(y\) | -6 | -4 | -2 | 0 |
| \(x\) = (9 + 2\(y\)): (\(y\)+3) | 1 | -1 | 5 | 3 |
| (\(x;y\)) | (1;-6) | (-1; -4) | (5;-2) | (3;0) |
Theo bảng trên ta có các cặp \(x;y\) nguyên thỏa mãn đề bài lần lượt là:
(1; -6); (-1; -4); (5; -2) ;(3; 0)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
26 tháng 12 2022
a, 3x ( y+1) + y + 1 = 7
(y+1)(3x +1) =7
th1 : \(\left\{{}\begin{matrix}y+1=1\\3x+1=7\end{matrix}\right.\) => \(\left\{{}\begin{matrix}y=0\\x=2\end{matrix}\right.\)
th2: \(\left\{{}\begin{matrix}y+1=-1\\3x+1=-7\end{matrix}\right.\)=> x = -8/3 (loại)
th3: \(\left\{{}\begin{matrix}y+1=7\\3x+1=1\end{matrix}\right.\)=> \(\left\{{}\begin{matrix}y=6\\x=0\end{matrix}\right.\)
th 4 : \(\left\{{}\begin{matrix}y+1=-7\\3x+1=-1\end{matrix}\right.\)=> x=-2/3 (loại)
Vậy (x,y)= (2 ;0); (0; 6)
b, xy - x + 3y - 3 = 5
(x( y-1) + 3( y-1) = 5
(y-1)(x+3) = 5
th1: \(\left\{{}\begin{matrix}y-1=1\\x+3=5\end{matrix}\right.\) => \(\left\{{}\begin{matrix}y=2\\x=8\end{matrix}\right.\)
th2: \(\left\{{}\begin{matrix}y-1=-1\\x+3=-5\end{matrix}\right.\) => \(\left\{{}\begin{matrix}y=0\\x=-8\end{matrix}\right.\)
th3: \(\left\{{}\begin{matrix}y-1=5\\x+3=1\end{matrix}\right.\) => \(\left\{{}\begin{matrix}y=6\\x=-2\end{matrix}\right.\)
th4: \(\left\{{}\begin{matrix}y-1=-5\\x+3=-1\end{matrix}\right.\) => \(\left\{{}\begin{matrix}y=-4\\x=-4\end{matrix}\right.\)
vậy (x, y) = ( 8; 2); ( -8; 0); (-2; 6); (-4; -4)
c, 2xy + x + y = 7 => y = \(\dfrac{7-x}{2x+1}\) ; y ϵ Z ⇔ 7-x ⋮ 2x+1
⇔ 14 - 2x ⋮ 2x + 1 ⇔ 15 - 2x - 1 ⋮ 2x + 1
th1 : 2x + 1 = -1=> x = -1; y = \(\dfrac{7-(-1)}{-1.2+1}\) = -8
th2: 2x+ 1 = 1=> x =0; y = 7
th3: 2x+1 = -3 => x = x=-2 => y = \(\dfrac{7-(-2)}{-2.2+1}\) = -3
th4: 2x+ 1 = 3 => x = 1 => y = \(\dfrac{7+1}{2.1+1}\) = 2
th5: 2x + 1 = -5 => x = -3=> y = \(\dfrac{7-(-3)}{-3.2+1}\) = -2
th6: 2x + 1 = 5 => x = 2; ; y = \(\dfrac{7-2}{2.2+1}\) =1
th7 : 2x + 1 = -15 => x = -8; y = \(\dfrac{7-(-8)}{-8.2+1}\) = -1
th8 : 2x+1 = 15 => x = 7; y = \(\dfrac{7-7}{2.7+1}\) = 0
kết luận
(x,y) = (-1; -8); (0 ;7); ( -2; -3) ; ( 1; 2); ( -3; -2); (2;1); (-8;-1);(7;0)
26 tháng 12 2022
3xy−2x+5y=293xy−2x+5y=29
9xy−6x+15y=879xy−6x+15y=87
(9xy−6x)+(15y−10)=77(9xy−6x)+(15y−10)=77
3x(3y−2)+5(3y−2)=773x(3y−2)+5(3y−2)=77
(3y−2)(3x+5)=77(3y−2)(3x+5)=77
⇒(3y−2)⇒(3y−2) và (3x+5)(3x+5) là Ư(77)=±1,±7,±11,±77Ư(77)=±1,±7,±11,±77
Ta có bảng giá trị sau:
Do x,y∈Zx,y∈Z nên (x,y)∈{(−4;−3),(−2;−25),(2;3),(24;1)}
x2−3x−xy+3y=7
=>(x2−xy)−(3x−3y)=7
=>x.(x−y)−3.(x−y)=7
=>(x−3).(x−y)=7
Ta có bảng sau