Từ một vị trí A tại cột đèn đỏ Bình điều khiển xe máy bắt đầu xuất phát chuyển động thẳng nhanh dần đều (NDĐ) thì bất ngờ phát hiện anh Cảnh Sát Giao Thông (CSGT) đứng ở phía trước (vị trí B) ra dấu hiệu dừng xe nên Bình đành phải giảm tốc độ cho xe chuyển động chậm dần đều (CDĐ) cho đến khi xe dừng lại trước mặt anh CSGT. Biết độ lớn gia tốc của hai giai đoạn chuyển động NDĐ và CDĐ là 0,4m/s2 và khoảng cách AB = 90m. Tính thời gian từ lúc xuất phát đến khi dừng lại trước mặt anh CSGT.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi gia tốc trong chuyển động nhanh dần đều của chất điểm A là a thì vận tốc của A là V A (t) = at. Tại thời điểm t = 8 ta có V A (8) = a . 8 = 6 ⇒ a = 3 4 m / s 2 Quãng đường A chuyển động được trong 8 giây đầu là
S 1 = ∫ 0 8 3 4 t d t = 3 8 t 2 0 8 = 24 m .
Thời gian A chuyển động đều cho đến lúc gặp B là 12 giây.
Quãng đường A đi được trong chuyển động đều là S 2 = 6 . 12 = 72m.
Quãng đường A đi được từ lúc xuất phát đến lúc gặp B là S = S 1 + S 2 = 24 + 72 = 96m
Gọi gia tốc của B là b thì vận tốc của B là v B (t) = bt
Quãng đường B đi được từ lúc xuất phát đến lúc gặp A là 96 m.
Ta có: S = ∫ 0 8 b t d t = b t 2 2 0 8 = 32b = 96 ⇒ b = 3 m / s 2
Vận tốc của B tại thời điểm gặp A là v B (8) = 3 . 8 = 24m/s
Đáp án C

Gọi gia tốc trong chuyển động nhanh dần đều của chất điểm A là a thì vận tốc của A là v A ( t ) = a t

Quãng đường A chuyển động được trong 8 giây đầu là
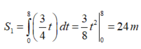
Thời gian A chuyển động đều cho đến lúc gặp B là 12 giây.
Quãng đường A đi được trong chuyển động đều là S 2 = 6 . 12 = 72 m
Quãng đường A đi được từ lúc xuất phát đến lúc gặp B là
S = S 1 + S 2 = 72 + 24 = 96
Gọi gia tốc của B là b thì vận tốc của B là v B ( t ) = b t
Quãng đường B đi được từ lúc xuất phát đến lúc gặp A là 96 m.
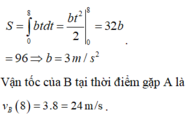
Đáp án C

Để giải bài toán này, ta sử dụng các công thức về vận tốc, thời gian và quãng đường đi được.
Cho ô tô chạy với vận tốc ban đầu v0 = 25 m/s và cảnh sát có gia tốc a = 6 m/s^2.
Ta có công thức vận tốc: v = v0 + at
Với v là vận tốc tại thời điểm t, v0 là vận tốc ban đầu, a là gia tốc và t là thời gian.
Ta xác định thời điểm và vị trí anh cảnh sát đuổi kịp ô tô.Để anh cảnh sát đuổi kịp ô tô, ta giải phương trình sau để tìm thời gian cần thiết: 25 + 6t = 0 (vận tốc ô tô) và 6t = 75 (quãng đường cảnh sát cần phải bắt kịp ô tô)
Ta giải phương trình 6t = 75 để tìm thời gian cần thiết: 6t = 75 t = 75/6 t ≈ 12.5 giây
Vậy sau khoảng 12.5 giây, anh cảnh sát sẽ đuổi kịp ô tô và cách vị trí xuất phát của anh cảnh sát là 75m.
Ta xác định thời điểm và vị trí anh cảnh sát đuổi kịp ô tô.Ta giải phương trình sau để tìm thời gian cần thiết: 25 + 6t = 0 (vận tốc ô tô) và 6t = 300 (quãng đường cảnh sát cần phải bắt kịp ô tô)
Ta giải phương trình 6t = 300 để tìm thời gian cần thiết: 6t = 300 t = 300/6 t = 50 giây
Vậy sau khoảng 50 giây, anh cảnh sát sẽ đuổi kịp ô tô và cách vị trí xuất phát của anh cảnh sát là 300m.
Do đó, đáp án là C. Sau 12s kể từ lúc anh cảnh sát xuất phát, cách vị trí xuất phát của anh cảnh sát 300m.

Tại vị trí gặp nhau của hai xe thì
Xe xuất phát từ A có vận tốc bằng
v 1 = a 1 t = 2,5. 10 - 2 .400 = 10(m/s) = 36(km/h)
Xe xuất phát từ B có vận tốc bằng
v 2 = a 2 t = 2,0. 10 - 2 .400 = 8(m/s) = 28,8(km/h)
Vì gia tốc của NDĐ và CDĐ bằng nhau và bằng 0,4m/s² nên thời gian tăng tốc và giảm tốc là bằng nhau và quãng đường tăng tốc và giảm tốc cũng bằng nhau và bằng 90/2=45m
Ta có thời gian tăng tốc là:
\(s=\frac{1}{2}at^2\rightarrow t=\sqrt{\frac{2s}{a}}=\sqrt{\frac{2.45}{0,4}}=15s\)
Thời gian từ lúc xuất phát đến khi dừng lại trước mặt anh CSGT là 2t=30s