1.Cho hình thoi ABCD có cạnh =a.Biết góc B=60 độ
a)C/m tam giác ABC đều
b)Tính diện tích hình thoi ABCD theo a
2.Cho hình vuông ABCD có độ dài cạnh =a.Điểm M bất kì trên đường thẳng AC.Kẻ ME vuông góc AB tại E và MF vuông góc AC tại F.Tìm vị trí của điểm M trên AC để diện tích tam giác CEF lớn nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Phương pháp tọa độ (cách này tính toán khá phức tạp nên chỉ nêu ra để học sinh thấy không phải bài toán nào cũng dùng phương pháp tọa độ cũng nhanh nhất)
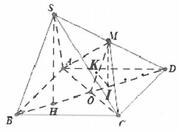
Ta chọn hệ trục tọa độ như hình vẽ và chọn a = 1.
Ta có:
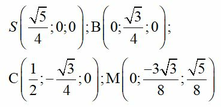

AB=21/(3+4)x3=9 cm
AC=21-9=12cm
Tự kẻ hình bạn nhé =)))
Áp dụng định lí Pitago vào tam giác ABC , có
AB^2+AC^2=BC^2
=>thay số vào, tính được BC=15cm
Áp dụng hệ thức giữa cạnh và đường cao trong tg vuông, có:
AB^2=BHxBC
=>BH=81/15=5.4cm
=>CH=15-5.4=9.6cm
AH^2=BHxCH=5.4x9.6=51.84cm

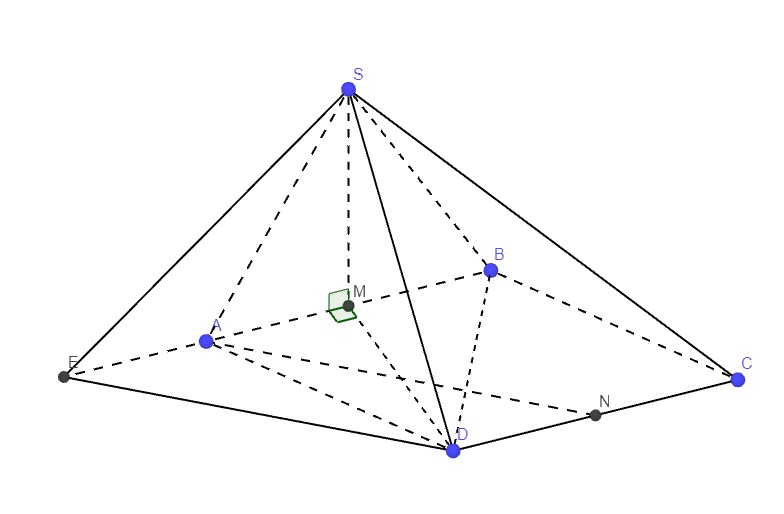
Gọi E là điểm đối xứng M qua A
\(\Rightarrow ANDE\) là hình bình hành (cặp cạnh đối AE và DN song song và bằng nhau)
\(\Rightarrow AN||DE\Rightarrow\) góc giữa AN và SD bằng góc giữa SD và DE
Do tam giác ABD đều \(\Rightarrow MD\perp AB\) \(\Rightarrow\Delta MDE\) vuông tại M
Do tam giác SAB đều \(\Rightarrow SM\perp AB\)
Mà \(\left(SAB\right)\perp\left(ABCD\right)\Rightarrow SM\perp\left(ABCD\right)\)
\(\Rightarrow\) Các tam giác SMD, SME vuông tại M
\(SM=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác SAB đều)
\(MD=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác ABD đều)
\(ME=2AM=AB=a\)
Pitago:
\(SD=\sqrt{SM^2+MD^2}=\dfrac{a\sqrt{6}}{2}\)
\(SE=\sqrt{SM^2+ME^2}=\dfrac{a\sqrt{7}}{2}\)
\(ED=\sqrt{MD^2+ME^2}=\dfrac{a\sqrt{7}}{2}\)
\(\Rightarrow cos\widehat{SDE}=\dfrac{SD^2+ED^2-SE^2}{2SD.ED}=\dfrac{\sqrt{42}}{14}\)

1) hình tự vẽ nhé
a) Vì ABCD là hình thoi (gt)
\(\Rightarrow AB=BC\left(đn\right)\)
\(\Rightarrow\Delta ABC\)cân tại B
Mà \(\widehat{B}=60^0\)
\(\Rightarrow\Delta ABC\)là tam giác đều
b) Vì \(\Delta ABC\)đều(cmt)\(\Rightarrow AB=BC=AC=a\)
Gọi O là giao điểm 2 đường chéo BD và AC
Vì ABCD là hình thoi (gt) \(\Rightarrow DB\perp AC\left(tc\right)\)
\(\Rightarrow BO\perp AC\)
Vì tam giác ABC đều mà trong tam giác ABC thì BO là đường cao ứng với cạnh AC
\(\Rightarrow BO\)là đường trung tuyến ứng vs cạnh AC(tc)
\(\Rightarrow O\)là trung điểm của AC
\(\Rightarrow AO=OC=\frac{1}{2}AC=\frac{1}{2}a\)
Áp dụng định lý Py-ta-go vào tam giác BOC vuông tại O ta được:
\(BO^2+OC^2=BC^2\)
\(BO^2+\frac{1}{4}a^2=a^2\)
\(BO^2=\frac{3}{4}a^2\)
\(\Rightarrow BO=\frac{\sqrt{3}}{2}a\)
Ta có: \(S_{ABC}=\frac{1}{2}BO.AC=\frac{1}{2}.\frac{\sqrt{3}a}{2}.a\)
\(=\frac{\sqrt{3}}{4}a^2\)
CMTT \(S_{ADC}=\frac{\sqrt{3}}{4}a^2\)
\(S_{ABCD}=S_{ADC}+S_{ABC}=\frac{\sqrt{3}}{2}a^2\)