Cho tứ giác ABCD nội tiếp được và có các cạnh a,b,c,d.
C/m: S= \(\sqrt{\left(p-a\right)\left(p-b\right)\left(p-c\right)\left(p-d\right)}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BT
18 tháng 5 2017
Muốn chứng minh tứ giác ABCD là tứ giác nội tiếp ta cần chứng minh: \(\widehat{ABC}+\widehat{ADC}=180^o\)\(\Leftrightarrow\)
\(\overrightarrow{BA}\left(-1;3\right);\overrightarrow{BC}\left(-2;-4\right)\)
\(cos\widehat{ABC}=cos\left(\overrightarrow{BA};\overrightarrow{BC}\right)\)\(=\dfrac{\left(-1\right).\left(-2\right)+3.\left(-4\right)}{\sqrt{\left(-1\right)^2+3^2}.\sqrt{\left(-2\right)^2+\left(-4\right)^2}}=\dfrac{-\sqrt{2}}{2}\).
Suy ra \(\overrightarrow{ABC}=135^o\).
\(\overrightarrow{DA}\left(4;-2\right);\overrightarrow{DC}\left(3;-9\right)\)
\(cos\widehat{ADC}=\left(\overrightarrow{DA};\overrightarrow{DC}\right)=\dfrac{4.3+\left(-2\right).\left(-9\right)}{\sqrt{4^2+2^2}.\sqrt{\left(3\right)^2+\left(-3\right)^2}}=\dfrac{\sqrt{2}}{2}\)
Suy ra \(\widehat{ADC}=45^o\)
Vậy \(\widehat{ADC}+\widehat{ABC}=135^o+45^o=180^o\).
Vì vậy tứ giác ABCD nội tiếp.
11 tháng 9 2023
Điểm \(A\left( { - 3;3} \right) \Rightarrow \) hoành độ là -3 và tung độ là 3.
Điểm \(B\left( {3;3} \right) \Rightarrow \) hoành độ là 3 và tung độ là 3.
Điểm \(C\left( {3; - 3} \right) \Rightarrow \) hoành độ là 3 và tung độ là -3.
Điểm \(D\left( { - 3; - 3} \right) \Rightarrow \) hoành độ là -3 và tung độ là -3.
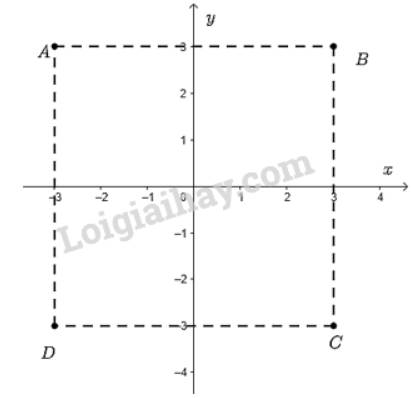
Các cạnh của tứ giác \(ABCD\) bằng nhau và các góc của tứ giác \(ABCD\) bằng nhau và bằng \(90^\circ \).
28 tháng 8 2020
Với mọi \(0\le a,b,c,d\le1\) thì \(\left(abcd\right)^{\frac{1}{3}}\le\left(abcvd\right)^{\frac{1}{4}}\) hay \(\sqrt[3]{abcd}\le\sqrt[4]{abcd}\)
Tương tự thì \(\sqrt[3]{\left(1-a\right)\left(1-b\right)\left(1-c\right)\left(1-d\right)}\le\sqrt[4]{\left(1-a\right)\left(1-b\right)\left(1-c\right)\left(1-d\right)}\)
\(\Rightarrow P\le\sqrt[4]{abcd}+\sqrt[4]{\left(1-a\right)\left(1-b\right)\left(1-c\right)\left(1-d\right)}\)
\(\le\frac{a+b+c+d}{4}+\frac{4-a-b-c-d}{4}=1\)
Đẳng thức xảy ra tại a=b=c=0 hoặc a=b=c=d=1
16 tháng 6 2015
a) phương trình
<=> x \(\in\) Z và x \(\le\) \(\frac{4x+1}{9}\) < x +1 (1)
(1) <=> 0 \(\le\) \(\frac{4x+1}{9}-x\) < 1
<=> 0 \(\le\) 4x + 1 - 9x < 9 <=> 0 \(\le\) 1 - 5x < 9 <=> \(-\frac{9}{5}\) < x \(\le\) \(\frac{1}{5}\)
Mà x nguyên nên x = -1; 0