Tìm m để pt sau có 2 nghiệm dương phân biệt:
1) ( m2+ m + 1) x2 + ( 2m - 3 0 x + m - 5 = 0
2) x2 - 6mx + 2 - 2m + 9m2 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 5 2021
Ta có: \(\Delta=\left(2m-1\right)^2-4\cdot1\cdot\left(m^2-2\right)\)
\(=4m^2-4m+1-4m^2+8\)
\(=-4m+9\)
Để phương trình có hai nghiệm phân biệt thì \(\Delta>0\)
\(\Leftrightarrow-4m+9>0\)
\(\Leftrightarrow-4m>-9\)
hay \(m< \dfrac{9}{4}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2m-1\\x_1\cdot x_2=m^2-2\end{matrix}\right.\)
Ta có: \(\left|x_1-x_2\right|=\sqrt{5}\)
\(\Leftrightarrow\sqrt{\left(x_1-x_2\right)^2}=\sqrt{5}\)
\(\Leftrightarrow\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=\sqrt{5}\)
\(\Leftrightarrow\left(2m-1\right)^2-4\cdot\left(m^2-2\right)=5\)
\(\Leftrightarrow4m^2-4m+1-4m^2+8=5\)
\(\Leftrightarrow-4m=-4\)
hay m=1(thỏa ĐK)
Vậy: m=1
13 tháng 5 2021
PT có 2 nghiệm phân biệt
`<=>Delta>0`
`<=>(2m-1)^2-4(m^2-2)>0`
`<=>4m^2-4m+1-4m^2+8>0`
`<=>-4m+9>0`
`<=>m<9/4`
Áp dụng vi-ét:`x_1+x_2=2m-1,x_1.x_2=m^2-2`
`|x_1-x_2|=\sqrt5`
`<=>(x_1-x_2)^2=5`
`<=>(x_1+x_2)^2-4(x_1.x_2)=5`
`<=>4m^2-4m+1-4m^2+8=5`
`<=>-4m+8=5`
`<=>4m=3`
`<=>m=3/4(tm)`
Vậy `m=3/4=>|x_1-x_2|=\sqrt5`
23 tháng 11 2021
\(1,\\ a,ĐK:m\ne1\\ \Delta=49+48\left(m-1\right)=48m+1\\ \text{PT vô nghiệm }\Leftrightarrow48m+1< 0\Leftrightarrow m< -\dfrac{1}{48}\\ \text{PT có nghiệm kép }\Leftrightarrow48m+1=0\Leftrightarrow m=-\dfrac{1}{48}\\ \text{PT có 2 nghiệm phân biệt }\Leftrightarrow48m+1>0\Leftrightarrow m>-\dfrac{1}{48};m\ne1\)
\(b,\Delta=4\left(m-1\right)^2+4\left(2m+1\right)=4m^2+8>0,\forall m\\ \text{Vậy PT có 2 nghiệm phân biệt với mọi m}\\ 2,\\ \text{PT có 2 nghiệm phân biệt }\)
\(\Leftrightarrow\Delta=4\left(m+1\right)^2-4\left(m^2-1\right)>0\\ \Leftrightarrow4m^2+8m+4-4m^2+4>0\\ \Leftrightarrow8m+8>0\\ \Leftrightarrow m>-1\)
4 tháng 8 2017
1.Ta có \(\Delta=4m^2-4\left(m^2-m-3\right)=4m+12\)
Để phương trình có 2 nghiệm phân biệt \(\Rightarrow\Delta>0\Rightarrow4m+12>0\Rightarrow m>-3\)
Theo hệ thức Viet ta có \(\hept{\begin{cases}x_1+x_2=2m\\x_1.x_2=m^2-m-3\end{cases}}\)
a. Phương trình có 2 nghiệm trái dấu \(\Rightarrow x_1.x_2< 0\Rightarrow m^2-m-3< 0\Rightarrow\frac{1-\sqrt{13}}{2}< m< \frac{1+\sqrt{13}}{2}\)
Vậy \(\frac{1-\sqrt{13}}{2}< m< \frac{1+\sqrt{13}}{2}\)
b. Phương trình có 2 nghiệm phân biệt dương \(\Leftrightarrow\hept{\begin{cases}x_1+x_2=2m>0\\x_1.x_2=m^2-m-3>0\end{cases}\Leftrightarrow\hept{\begin{cases}m>0\\m< \frac{1-\sqrt{13}}{2}\end{cases}\left(l\right);\hept{\begin{cases}m>0\\m>\frac{1+\sqrt{13}}{2}\end{cases}\Leftrightarrow m>\frac{1+\sqrt{13}}{2}}}}\)
Vậy \(m>\frac{1+\sqrt{13}}{2}\)
2. a.Ta có \(\Delta=\left(2m-1\right)^2+4m=4m^2-4m+1+4m=4m^2+1\)
Ta thấy \(\Delta=4m^2+1>0\forall m\)
Vậy phương trình luôn có 2 nghiejm phân biệt với mọi m
b. Theo hệ thức Viet ta có \(\hept{\begin{cases}x_1+x_2=1-2m\\x_1.x_2=-m\end{cases}}\)
Để \(x_1-x_2=1\Leftrightarrow\left(x_1-x_2\right)^2=1\Leftrightarrow\left(x_1+x2\right)^2-4x_1x_2=1\)
\(\Leftrightarrow\left(1-2m\right)^2-4.\left(-m\right)=1\Leftrightarrow4m^2-4m+1+4m=1\)
\(\Leftrightarrow m^2=0\Leftrightarrow m=0\)
Vậy \(m=0\)thoă mãn yêu cầu bài toán
CV
1
Y
7 tháng 4 2023
Để pt có 2 nghiệm pb thì \(\Delta\ge0\)
\(\Leftrightarrow\Delta\ge0\)
Ta có : \(\Delta=b^2-4ac=\left[-\left(2m-3\right)\right]^2-4\left(-m+2\right)\ge0\)
\(\Leftrightarrow\left(2m-3\right)^2+4m-8\ge0\)
\(\Leftrightarrow4m^2-12m+9+4m-8\ge0\)
\(\Leftrightarrow4m^2-8m+1\ge0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{2+\sqrt{3}}{2}\\m=\dfrac{2-\sqrt{3}}{2}\end{matrix}\right.\)
CM
17 tháng 2 2018
Phương trình đã cho có hai nghiệm dương x 1 , x 2 phân biệt khi và chỉ khi
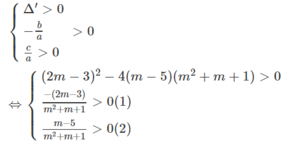
Vì m 2 + m + 1 > 0 nên bất phương trình (1) ⇔ m < 3/2 và bất phương trình (2) ⇔ m > 5
Do dó không có giá trị của m thỏa mãn yêu cầu bài toán
CM
26 tháng 4 2017
Phương trình x 2 + (2m – 1)x + m 2 – 2m + 2 = 0
(a = 1; b = 2m – 1; c = m 2 – 2m + 2)
Ta có ∆ = ( 2 m – 1 ) 2 – 4 . ( m 2 – 2 m + 2 ) = 4 m – 7
Gọi x 1 ; x 2 là hai nghiệm của phương trình, theo hệ thức Vi-ét ta có
Vì a = 1 ≠ 0 nên phương trình có hai nghiệm âm phân biệt ⇔ Δ > 0 P > 0 S > 0
⇔ 4 m − 7 > 0 1 − 2 m > 0 m 2 − 2 m + 2 > 0 ⇔ m > 7 4 m < 1 2 m − 1 2 + 1 > 0 ( l u o n d u n g ) ⇔ m > 7 4 m < 1 2 ( v o l y )
Vậy không có giá trị nào của m thỏa mãn đề bài
Đáp án: D
LG
0