Cho hình vuông ABCD. Các điểm E,F thỏa mãn: \(2\overrightarrow{EB}+\overrightarrow{EC}=\overrightarrow{0}\)và \(2\overrightarrow{CF}+\overrightarrow{CD}=\overrightarrow{0}\)
Gọi I là giao của BF và AE Chứng minh rằng : tam giác AIC vuông.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
Ta có \(AC = AB\sqrt 2 = a\sqrt 2 \)
+) \(\overrightarrow {KA} + \overrightarrow {KC} = \overrightarrow 0 \),
Suy ra K là trung điểm AC \( \Rightarrow AK = \frac{1}{2}.a\sqrt 2 = \frac{{a\sqrt 2 }}{2}\)
+) \(\overrightarrow {HA} + \overrightarrow {HD} + \overrightarrow {HC} = \overrightarrow 0 \), suy ra H là trọng tâm của tam giác ADC
\(\Rightarrow DH = \frac{2}{3}DK = \frac{1}{3}DB\) (1)
+) \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \), suy ra G là trọng tâm của tam giác ABC
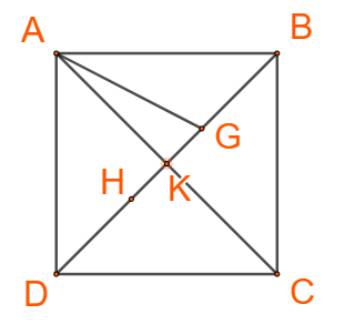
\(\Rightarrow BG = \frac{2}{3}BK = \frac{1}{3}BD\) (2)
\((1,2) \Rightarrow HG = \frac{1}{3}BD=\frac{{a\sqrt 2 }}{3}\)
Mà \(KG = KH = \frac{1}{2}HG= \frac{{a\sqrt 2 }}{6}\) (2)
\(\Rightarrow AG = \sqrt {A{K^2} + G{K^2}} = \sqrt {{{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 2 }}{6}} \right)}^2}} = \frac{{a\sqrt 5 }}{3}\)
\( \Rightarrow \left| {\overrightarrow {AG} } \right| = \frac{{a\sqrt 5 }}{3}\)
Vậy \(\left|\overrightarrow {KA}\right| =\frac{{a\sqrt 2 }}{2} ,\left|\overrightarrow {GH}\right|=\frac{{a\sqrt 2 }}{3} ,\left|\overrightarrow {AG}\right|=\frac{{a\sqrt 5 }}{3} \).
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
Ta có:
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \Leftrightarrow \left( {\overrightarrow {GI} + \overrightarrow {IA} } \right) + \left( {\overrightarrow {GI} + \overrightarrow {IB} } \right) + \left( {\overrightarrow {GJ} + \overrightarrow {JC} } \right) + \left( {\overrightarrow {GJ} + \overrightarrow {JD} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow 2\overrightarrow {GI} + \left( {\overrightarrow {IA} + \overrightarrow {IB} } \right) + 2\overrightarrow {GJ} + \left( {\overrightarrow {JC} + \overrightarrow {JD} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow 2\overrightarrow {GI} + 2\overrightarrow {GJ} = \overrightarrow 0 \Leftrightarrow 2\left( {\overrightarrow {GI} + \overrightarrow {GJ} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {GI} + \overrightarrow {GJ} = \overrightarrow 0 \Rightarrow \)G là trung điểm của đoạn thẳng IJ
Vậy I, G, J thẳng hàng
AH
Akai Haruma
Giáo viên
15 tháng 7 2017
Lời giải:
Dễ thấy \(\triangle AEO=\triangle CFO(g.c.g)\)
suy ra \(\frac{AO}{OC}=\frac{EO}{OF}=1\Rightarrow \) $O$ là trung điểm của $EF$
Do đó \(\overrightarrow{OE}+\overrightarrow{OF}=\overrightarrow{0}\)
Ta có \(AE\parallel CF\) và chiều vector ngược nhau, suy ra \(\overrightarrow{AE}\uparrow\downarrow \overrightarrow {CF}\)
Từ hai tam giác bằng nhau trên cũng suy ra \(AE=CF\)
Do đó \(\overrightarrow{AE}+\overrightarrow{CF}=\overrightarrow{0}\) Vì \(AE=CF,AB=CD\Rightarrow EB=DF\). Từ đó dễ thấy \(BEDF\) là hình bình hành Ta có \(\overrightarrow{DE};\overrightarrow{BF}\) là hai vector ngược hướng và có độ dài bằng nhau nên \(\overrightarrow{DE}+\overrightarrow{BF}=\overrightarrow{0}\)
AH
Akai Haruma
Giáo viên
10 tháng 10 2021
Lời giải:
\(\overrightarrow{JA}+2\overrightarrow{JB}+3\overrightarrow{JC}=\overrightarrow{0}\)
\(\Leftrightarrow \overrightarrow{JA}+2(\overrightarrow{JA}+\overrightarrow{AB})+3(\overrightarrow{JA}+\overrightarrow{AC})=\overrightarrow{0}\)
\(\Leftrightarrow 6\overrightarrow{JA}+2\overrightarrow{AB}+3\overrightarrow{AC}=\overrightarrow{0}\)
\(\Leftrightarrow \overrightarrow{AJ}=\frac{2\overrightarrow{AB}+3\overrightarrow{AC}}{6}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
a) Ta có: \(\overrightarrow {EA} + \overrightarrow {EB} + \overrightarrow {EC} + \overrightarrow {ED} \)\( = 4\overrightarrow {EG} + \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} \)
Mà: \(\overrightarrow {GA} + \overrightarrow {GB} = 2\overrightarrow {GM} ;\) (do M là trung điểm của AB)
\(\overrightarrow {GC} + \overrightarrow {GD} = 2\overrightarrow {GN} \) (do N là trung điểm của CD)
\( \Rightarrow \overrightarrow {EA} + \overrightarrow {EB} + \overrightarrow {EC} + \overrightarrow {ED} = 4\overrightarrow {EG} + 2(\overrightarrow {GM} + \overrightarrow {GN} ) = 4\overrightarrow {EG} \) (do G là trung điểm của MN)
b) Vì E là trọng tâm tam giác BCD nên \(\overrightarrow {EB} + \overrightarrow {EC} + \overrightarrow {ED} = \overrightarrow 0 \)
Từ ý a ta suy ra \(\overrightarrow {EA} = 4\overrightarrow {EG} \)
c) Ta có: \(\overrightarrow {EA} = 4\overrightarrow {EG} \Leftrightarrow \overrightarrow {EA} = 4.(\overrightarrow {EA} + \overrightarrow {AG} ) \Leftrightarrow - 3\overrightarrow {EA} = 4\overrightarrow {AG} \)
\( \Leftrightarrow 3\overrightarrow {AE} = 4\overrightarrow {AG} \) hay \(\overrightarrow {AG} = \frac{3}{4}\overrightarrow {AE} \)
Suy ra A, G, E thẳng hàng và \(AG = \frac{3}{4}AE \) nên G thuộc đoạn AE.