tam giác ABC có O là tâm đường tròn nội tiếp. E, F, D lần lượt là các tiếp điểm trên AB, BC, CA. Từ O kẻ đường thẳng song song với BC cắt AC tại I. chứng minh AI=BD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DV
Dương Việt My Anh
26 tháng 12 2019
Đúng(0)
Những câu hỏi liên quan
CM
18 tháng 2 2018
2) Theo 1). dễ thấy Δ B F A ∽ Δ B N P ⇒ Δ B N F ∽ Δ B P A ⇒ B N B P = F N A P (1).
Tương tự Δ C M E ∽ Δ C P A ⇒ C M C P = E M A P (2).
Từ (1) và (2), ta có B N C M ⋅ C P B P = F N E M và theo giả thiết F N E M = B N C M , suy ra C P = B P ⇒ A D là phân giác góc B A C ^ .
CM
1 tháng 11 2017
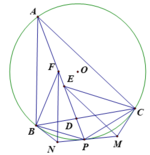
1). Gọi AD cắt (O) tại P khác A
Ta có P C M ^ = P A C ^ (góc tạo bởi tiếp tuyến và dây cung) = P E M ^ (góc đồng vị do E M ∥ A C );
Suy ra tứ giác ECMP nội tiếp. Từ đó suy ra M P C ^ = M E C ^ = E C A ^ = C A P ^ ⇒ PM tiếp xúc (O)
Tương tự PN tiếp xúc (O), suy ra MN tiếp xúc (O) tại P.