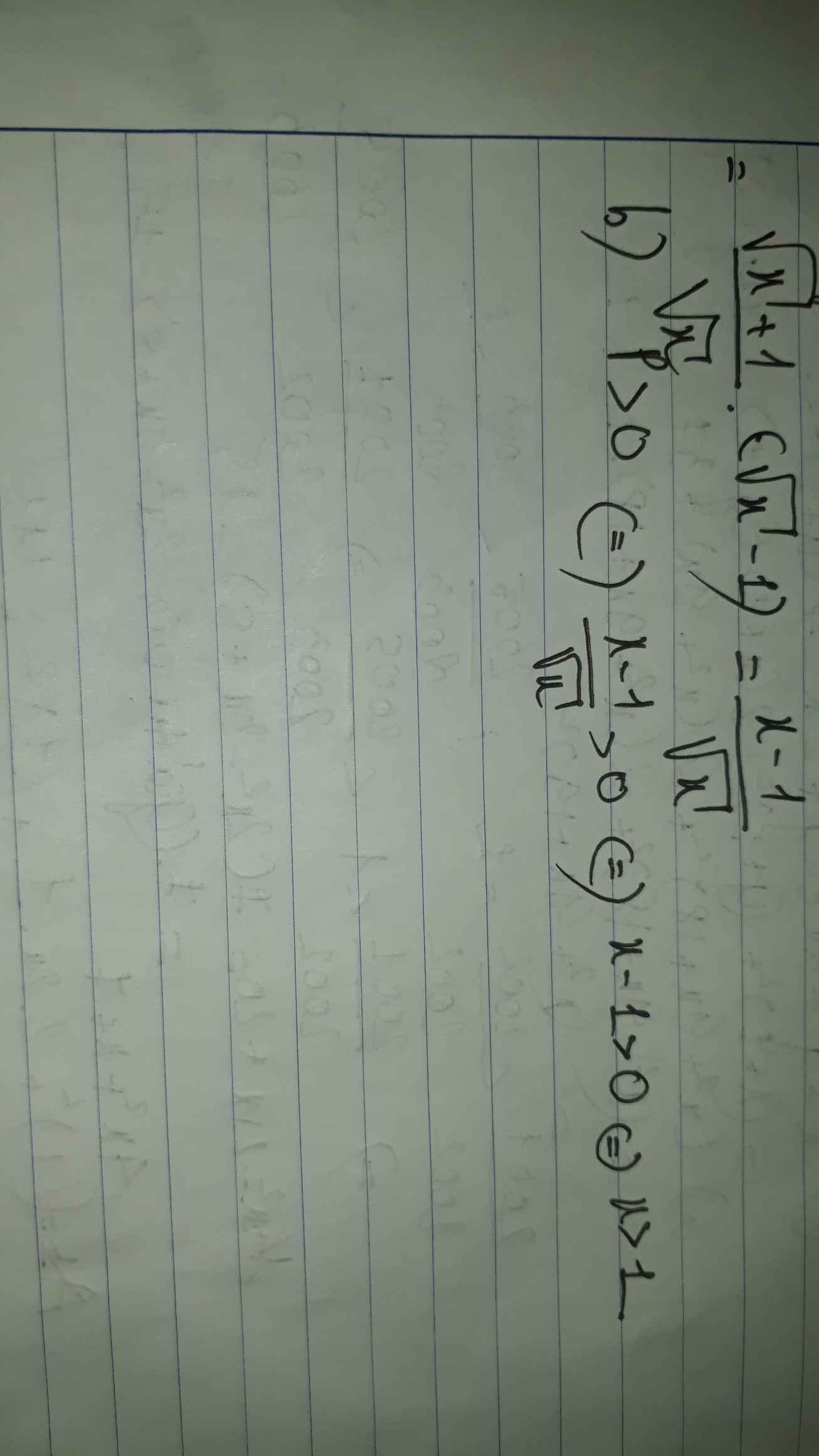Cho mình hỏi bài này ạ:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


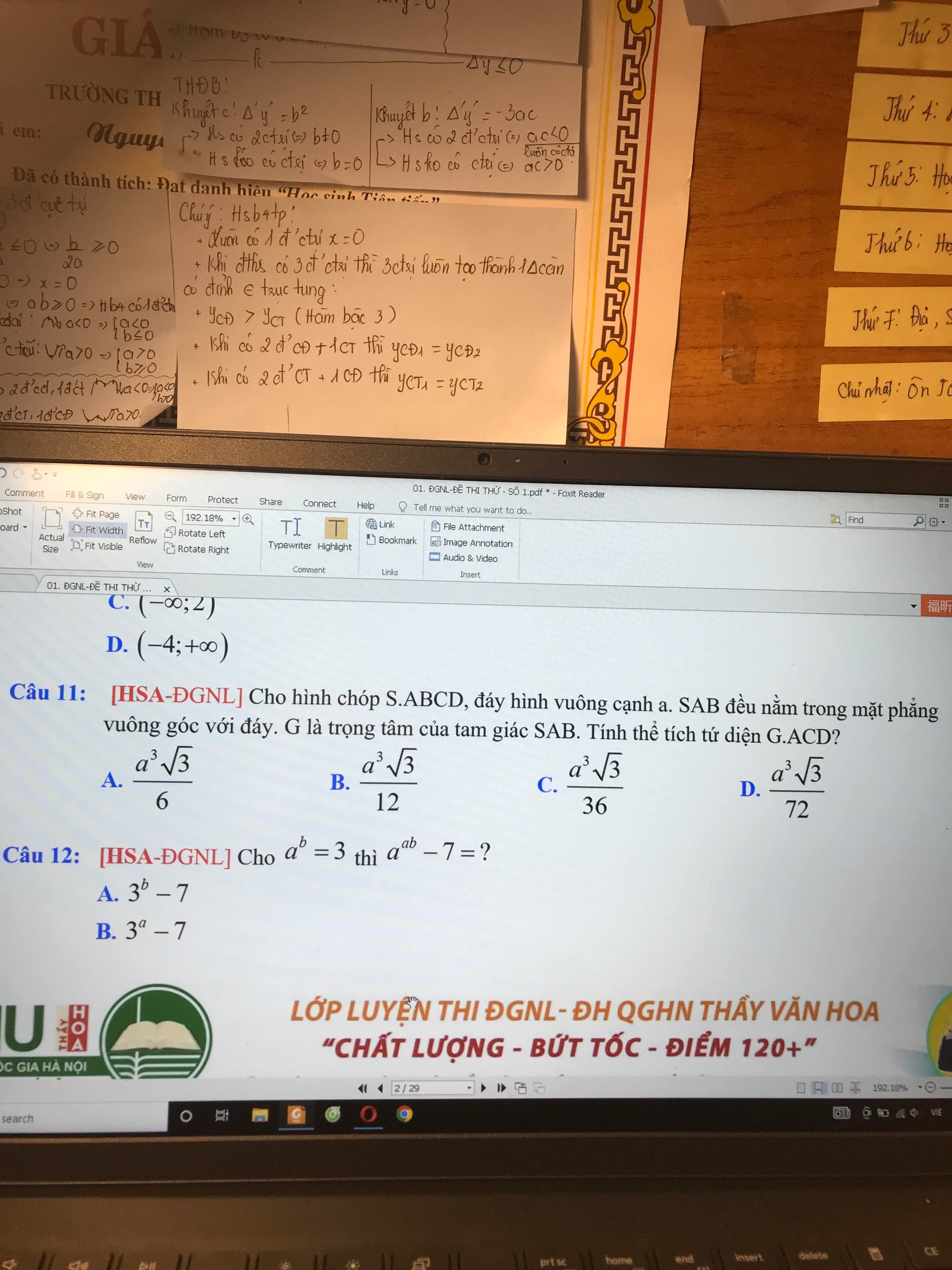
\(d\left(G;\left(ABCD\right)\right)=\dfrac{1}{3}d\left(S;\left(ABCD\right)\right)=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{6}\)
\(S_{\Delta ACD}=\dfrac{1}{2}S_{ABCD}=\dfrac{a^2}{2}\)
\(\Rightarrow V=\dfrac{1}{3}.\dfrac{a^2}{2}.\dfrac{a\sqrt{3}}{6}=\dfrac{a^3\sqrt{3}}{36}\)

a,mấy đoạn dấu : dấu+ trong đề hơi khó nhìn
\(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\right)\)
\(P=\left[\dfrac{\sqrt{x}.\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right]:\left(\dfrac{\sqrt{x}-1+2}{x-1}\right)\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{x-1}=\dfrac{\sqrt{x}+1}{\sqrt{x}}:\dfrac{1}{\sqrt{x}-1}=\dfrac{x-1}{\sqrt{x}}\)
b, \(P>0=>\dfrac{x-1}{\sqrt{x}}>0=>x-1>0< =>x>1\)(tm)
Vậy \(x>1\) .....
\(\)



a)\(42-15+28-5+20\)
\(=20-\left(15+5\right)+\left(42+28\right)\)
\(=20-20+70\)
\(=0+70\)
\(=70\)
b)\(\left(8\times5-40\right):\left(2+4+6+8+...+32+34\right)\)
\(=\left(40-40\right):\left(2+4+6+8+...+32+34\right)\)
\(=0:\left(2+4+6+8+...32+34\right)\)
\(=0\)

3.
Do M là trung điểm BC \(\Rightarrow\overrightarrow{CM}=\dfrac{1}{2}\overrightarrow{CB}\)
N là trung điểm AC \(\Rightarrow\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AC}\)
K là trung điểm AB \(\Rightarrow\overrightarrow{BK}=\dfrac{1}{2}\overrightarrow{BA}\)
Do đó:
\(\overrightarrow{AN}+\overrightarrow{CM}-\overrightarrow{KB}=\overrightarrow{AN}+\overrightarrow{CM}+\overrightarrow{BK}=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CB}+\dfrac{1}{2}\overrightarrow{BA}\)
\(=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BA}=\overrightarrow{0}\)
4.
\(\overrightarrow{BC}=\left(6;-2\right)\)
Gọi \(A'\left(x;y\right)\Rightarrow\overrightarrow{BA'}=\left(x+3;y-1\right)\)
Do A' thuộc BC \(\Rightarrow\overrightarrow{BA'}\) và \(\overrightarrow{BC}\) cùng phương
\(\Rightarrow\dfrac{x+3}{6}=\dfrac{y-1}{-2}\Rightarrow x=-3y\)
\(\Rightarrow A'\left(-3y;y\right)\Rightarrow\overrightarrow{AA'}=\left(-3y-2;y-4\right)\)
Mà AA' vuông góc BC \(\Rightarrow\overrightarrow{AA'}.\overrightarrow{BC}=0\)
\(\Rightarrow6\left(-3y-2\right)-2\left(y-4\right)=0\Rightarrow y=-\dfrac{1}{5}\)
\(\Rightarrow A'\left(\dfrac{3}{5};-\dfrac{1}{5}\right)\)

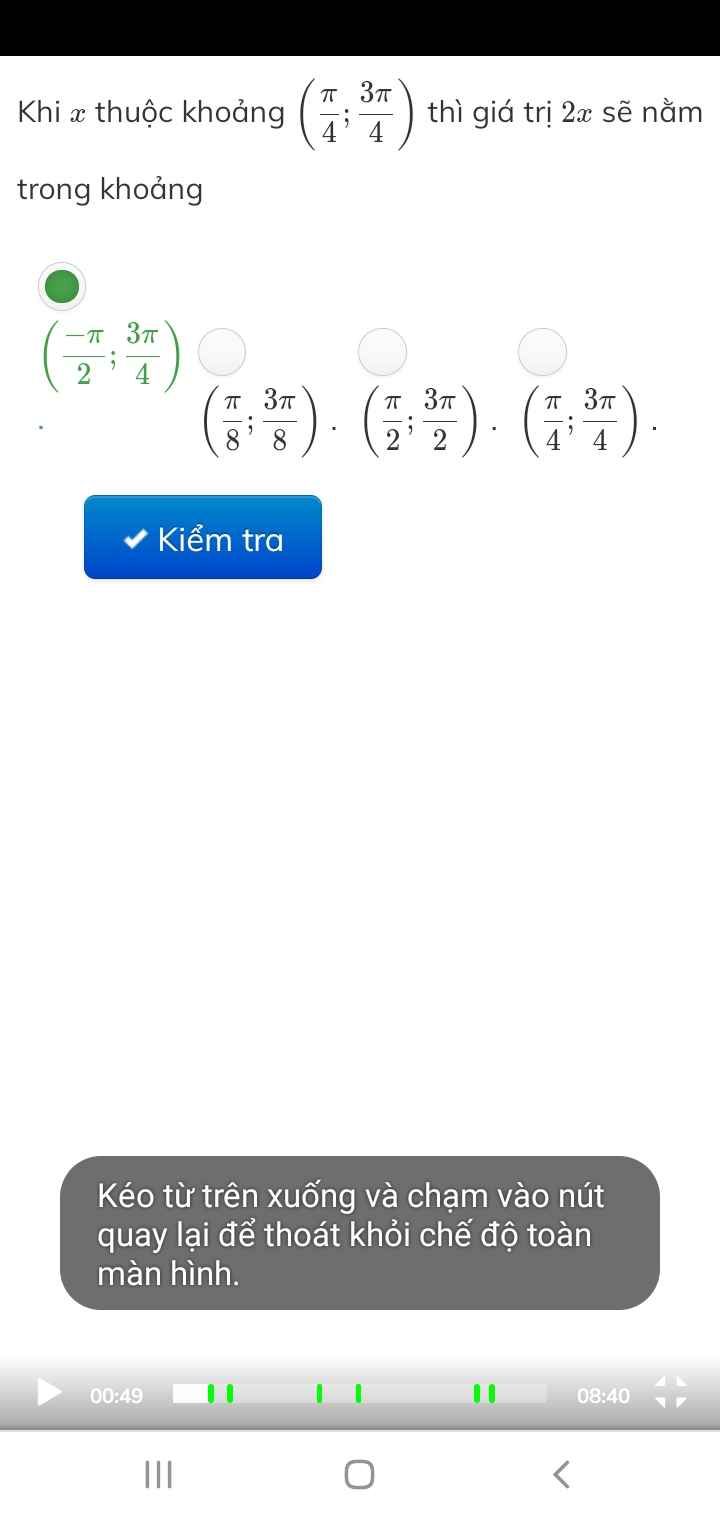
\(x\in\left(\dfrac{\pi}{4};\dfrac{3\pi}{4}\right)\Rightarrow2x\in\left(\dfrac{\pi}{2};\dfrac{3\pi}{2}\right)\)