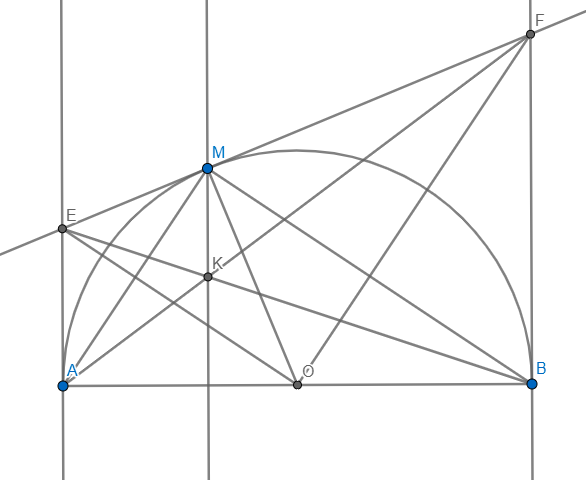
Cho nửa đường tròn (O, AB/2) . Kể tiếp tuyến Ax By với nửa đường tròn . Gọi C là 1 điểm trên nửa đường tròn . Qua C kẻ tiếp tuyến với nửa đường tròn cắt Ax By lần lượt ở E và F . Chứng minh
a EF = AE + BF
b Tam giác EOF vuông tại O
c Cho AE = 2R . Tính BF và chu vi ABFE
d BC cắt Ax tại K . Chứng minh Ok vuông góc với AE