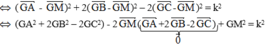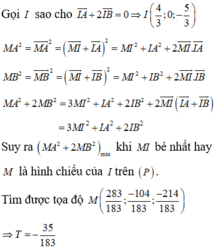Cho 2 điểm A và B cố định,AB=6. Tập hợp các điểm M thỏa mãn MA2+2MB2=36
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi T là điểm thỏa mãn : \(\overrightarrow{TA}+2\overrightarrow{TB}=\overrightarrow{0}\) \(\Rightarrow\overrightarrow{TA}=-2\overrightarrow{TB}\Rightarrow TA=2TB\) (2 vecto này cùng phương và cùng điểm đầu nên cùng thuộc AB) \(\Rightarrow TA=\dfrac{8}{3};TB=\dfrac{4}{3}\)
\(MA^2+2MB^2=30\Rightarrow3MT^2+TA^2+TB^2=30\Rightarrow3MT^2=\dfrac{190}{9}\Rightarrow MT=\sqrt{\dfrac{190}{27}}\) \(\Rightarrow\) Quỹ tích điểm M là đường tròn \(\left(T;\sqrt{\dfrac{190}{27}}\right)\)


Vì E ; F là hai điểm cố định nên từ đẳng thức (*) suy ra tập hợp các điểm M là trung trực của đoạn thẳng EF.
Gọi I là trung điểm của AB suy ra I cũng là trung điểm của EF.
Vậy tập hợp các điểm M thỏa mãn 2 M A → + M B → = M A → + 2 M B → là đường trung trực của đoạn thẳng AB.
Chọn A.

Chọn điểm E thuộc đoạn AB sao cho EB = 2EA ⇒ 2 E A → + E B → = 0 → .
Chọn điểm F thuộc đoạn AB sao cho FA = 2FB ⇒ 2 F B → + F A → = 0 → .
Ta có
2 M A → + M B → = M A → + 2 M B → ⇔ 2 M E → + 2 E A → + M E → + E B → = M F → + F A → + 2 M F → + 2 F B →
⇔ 3 M E → + 2 E A → + E B → ⏟ 0 → = 3 M F → + F A → + 2 F B → ⏟ 0 → ⇔ 3 M E → = 3 M F → ⇔ M E = M F . ( * )
Vì E ; F là hai điểm cố định nên từ đẳng thức (*) suy ra tập hợp các điểm M là trung trực của đoạn thẳng EF.
Gọi I là trung điểm của AB suy ra I cũng là trung điểm của EF
Vậy tập hợp các điểm M thỏa mãn 2 M A → + M B → = M A → + 2 M B → là đường trung trực của đoạn thẳng AB.
Chọn A.

Chọn D.
Gọi điểm M có tọa độ là ( x; y)
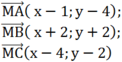
MA2 + 2MB2 + 3MC2
= (x - 1)2 + (y - 4)2 + 2[ (x + 2)2 + (y + 2)2] + 3[ (x - 4)2 + (y - 2)2]
= 6x2-18x + 6y2 + 93 = 1,5. (2x - 3)2 + 6(y - 1)2 + 147/2 ≥ 147/2
Dấu “=” xảy ra khi x = 1,5 và y = 1
Vậy tọa độ điểm M cần tìm là ( 1,5; 1).