Cho tam giác ABC , M là trung điểm của BC . Trên tia đối của tia MA lấy điểm E sao cho ME = MA . Chứng minh rằng :a) AC = EB và AC song song BEb) Gọi I là một điểm trên AC ; K là 1 điểm trên EB sao cho AI = EK . chứng minh 3 điểm I , M , K , thẳng hàngc) Từ E kẻ EH vuông góc BC ( H thuộc BC ) Biết góc HBE = 50 độ , góc MEB = 25 độ . Tính góc HEM và góc BME.Vẽ hình nha!Cần gấp ạ,ai nhanh nhất tớ tk...
Đọc tiếp
Cho tam giác ABC , M là trung điểm của BC . Trên tia đối của tia MA lấy điểm E sao cho ME = MA . Chứng minh rằng :
a) AC = EB và AC song song BE
b) Gọi I là một điểm trên AC ; K là 1 điểm trên EB sao cho AI = EK . chứng minh 3 điểm I , M , K , thẳng hàng
c) Từ E kẻ EH vuông góc BC ( H thuộc BC ) Biết góc HBE = 50 độ , góc MEB = 25 độ . Tính góc HEM và góc BME.
Vẽ hình nha!
Cần gấp ạ,ai nhanh nhất tớ tk cho!
AC // BE
. Biết 
= 50o ; 
=25o .
và 
. CMR: 
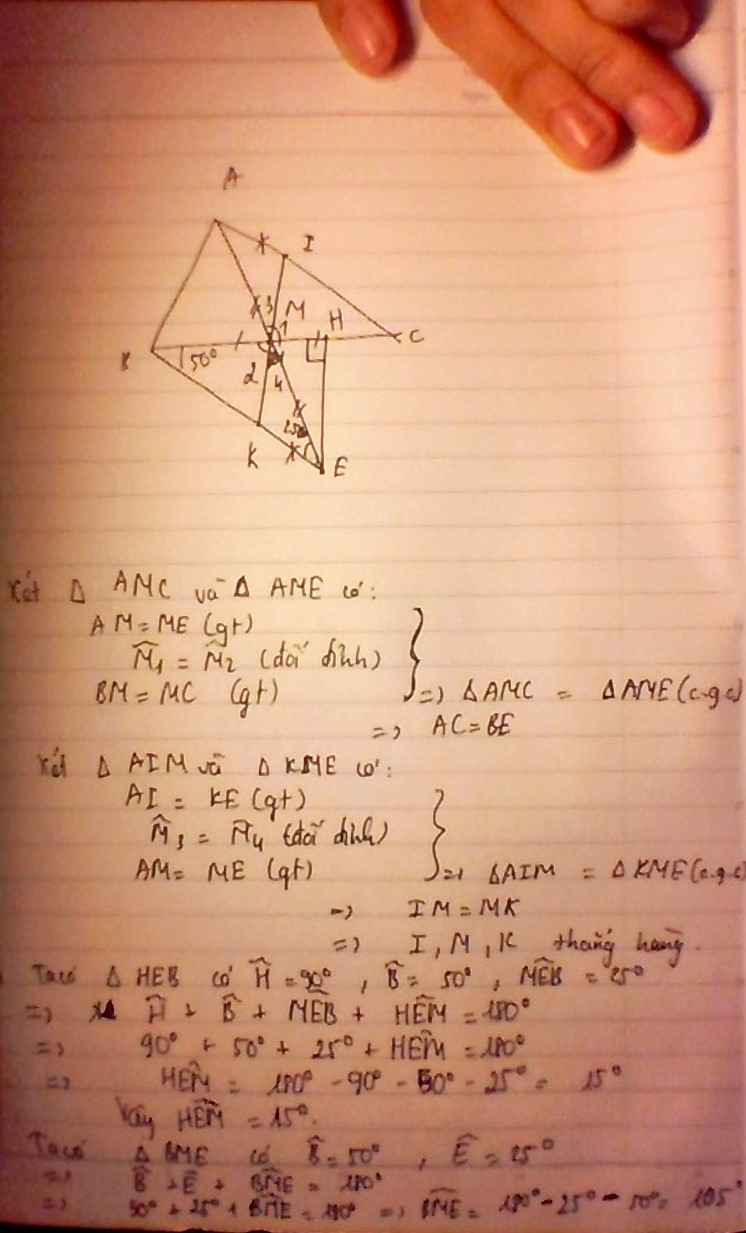
a) Xét ΔAMC;ΔBMEΔAMC;ΔBME có :
BM=MC(gt)BM=MC(gt)
AMCˆ=EMBˆAMC^=EMB^ (đối đỉnh)
AM=ME(gt)AM=ME(gt)
=> ΔAMC=ΔEMB(c.g.c)ΔAMC=ΔEMB(c.g.c)
=> AC=BEAC=BE (2 cạnh tương ứng)
=> BEMˆ=AMCˆBEM^=AMC^ (2 góc tương ứng)
Mà :2 góc này ở vị trí so le trong
=> AC //BE(đpcm)AC //BE(đpcm)
b) Xét ΔAMI;ΔEMKΔAMI;ΔEMK có :
AM=ME(gt)AM=ME(gt)
MAIˆ=MEKˆ(slt)MAI^=MEK^(slt)
AI=EK(gt)AI=EK(gt)
=> ΔAMI=ΔEMK(c.g.c)ΔAMI=ΔEMK(c.g.c)
=> KM=MIKM=MI (2 cạnh tương ứng)
=> M là trung điểm của KI
Do đó : I, M, K thẳng hàng (đpcm)
XIN LỖI VÌ TRÊN ĐÂY MÌNH KHÔNG BIẾT CÁCH VẼ HÌNH
Phần c nữa cậu ạ