Cho hình bình hành ABCD , BC=2AB . M là trung điểm của BC , N là trung điểm của của AD . AM cắt BN tại P , MD cắt CN tại Q
a, Chứng minh MCDN là hình thoi
b, Chứng minh ∆BNC vuông
c, Cho BN cắt CD tại K .Chứng minh BMDK là hình thang cân
d, Hình bình hành ABCD cần điều kiện gì để PMNQ là hình vuông
e,Chứng minh PMQN là hình chữ nhật
gấppp!!! Giúp mình với !!!

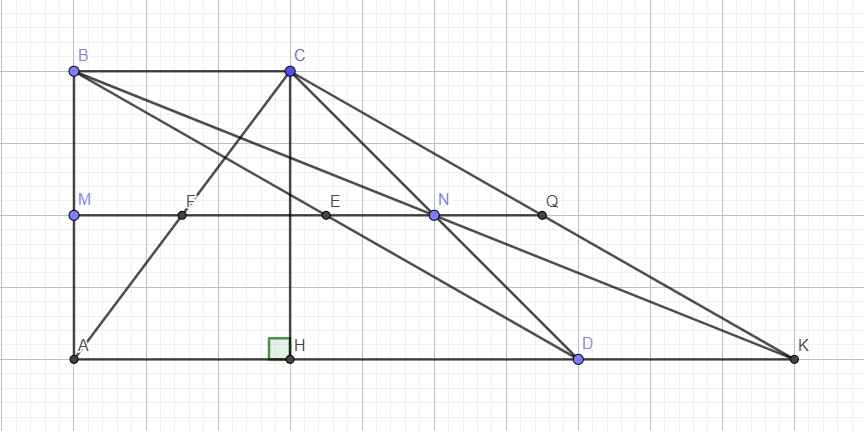
giúp mình với