Cho G và G' lần lượt là trọng tâm của tam giác ABC và A'B'C' Tính tổng vecto AA'+BB'+CC'
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 9 2015
chưa học trả lời làm gì cho mất thời gian mất công bạn Thanh Trang Hoàng phải đọc
CM
2 tháng 4 2019
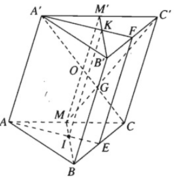
Gọi M và M’ tương ứng là trung điểm của AC và A’C’, ta có:
I ∈ BM, G ∈ C′M, K ∈ B′M′
Theo tính chất trọng tâm của tam giác ta có:
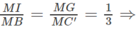
Ta có :
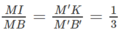
Mặt khác IG và IK ⊂ (IGK) nên (IGK) // (BB′C′C)
b) Gọi E và F tương ứng là trung điểm của BC và B’C’, O là trung điểm của A’C. A, I, E thẳng hàng nên (AIB’) chính là (AEB’). A’, G, C thẳng hàng nên (A’GK) chính là (A’CF).
Ta có B′E // CF (do B’FCE là hình bình hành ) và AE // A′F nên (AIB′) // (A′GK).
LA
13 tháng 3 2018
- Gọi G là trọng tâm \(\Delta ABC\), trung tuyến BE cắt A'C tại E'.
- Gọi trung điểm B'C' là D'. BE và D'C là đường trung bình của \(\Delta CAB'\)và \(\Delta C'AB'\)
=> BE // D'C và BE = D'C
Trung tuyến AD là đường trung bình của \(\Delta BCA'\Rightarrow GE'=BG=\frac{2}{3}\cdot BE=\frac{2}{3}\cdot D'C\)
Gọi G' là giao của A'D' và BE' ta có:
Áp dụng định lí Talet:
\(\frac{G'E'}{D'C}=\frac{A'E'}{A'C}=\frac{AG}{AD}=\frac{2}{3}\) (AD // A'C do là đường trung bình của \(\Delta BA'C\))
\(\Rightarrow G'E'=\frac{2}{3}\cdot D'C\)
=> G'E' = GE'.
Do G và G' cùng nằm trên BE' và G, G' nằm cùng phía so với E' nên G và G' trùng nhau.
Như vậy trung tuyến A'D' đi qua G, tương tự trung tuyến B'M' cũng đi qua G
=> G là trọng tâm của \(\Delta A'B'C'\)
"Nếu G là trọng tâm \(\Delta ABC\) thì vtGA + vtGB + vtGC = vt0"
Gọi giao của AG và BC là D. Trên AD kéo dài lấy E sao cho
DE = DG => GE = GA => vtGE = - vtGA.
Do GE và BC cắt nhau tại trung điểm D của chúng nên BGCE là hình bình hành
=> vtGB + vtGC = vtGE = -vtGA => vtGA + vtGB + vtGC = vt0
Gọi G là trọng tâm ABC, G' là trọng tâm \(\Delta A'B'C'\)
=> vtGA + vtGB + vtGC = vt0, vtG'A' + vtG'B' + vtG'C' = vt0
=> vt0 = (vtG'G + vtGA + vtAA') + (vtG'G + vtGB + vtBB') + (vtG'G + vtGC + vtCC')
=3vtG'G + (vtGA + vtGB + vtGC) + (vtBA + vtCB + vtAC)
=3vtG'G + vt0 + (vtBA + vtAC + vtCB) = 3vtG'G + vt0
=> vtG'G = vt0
=> G' trùng với G
CM
12 tháng 1 2017
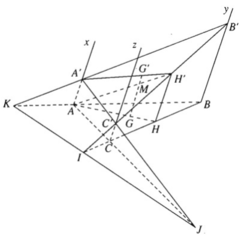
a) CC′ // BB′ ⇒ ΔICC′ ∼ ΔIBB′
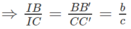
CC′ // AA′ ⇒ ΔJCC′ ∼ ΔJAA′
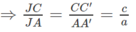
AA′ // BB′ ⇒ ΔKAA′ ∼ ΔKBB′
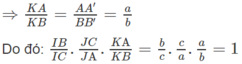
b) Gọi H và H’ lần lượt là trung điểm của các cạnh BC và B’C’. Vì HH’ là đường trung bình của hình thang BB’CC’ nên HH′ // BB′.
Mà BB′ // AA′ suy ra HH′ // AA′
Ta có: G ∈ AH và G′ ∈ A′H′ và ta có:
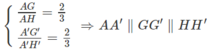
c) AH′ ∩ GG′ = M ⇒ GG′ = G′M + MG
Ta có: G′M // AA′ ⇒ ΔH′G′M ∼ ΔH′A′A
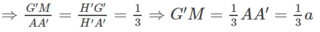
MG // HH′ ⇒ ΔAMG ∼ ΔAH′H
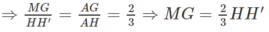
Mặt khác HH’ là đường trung bình của hình thang BB’CC’ nên
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 12 2020
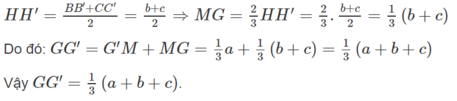
Ta có:
\(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\)
Mà \(\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
\(\dfrac{1}{3}\left(\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}\right)=\dfrac{1}{3}\left(\overrightarrow{AG}+\overrightarrow{GG'}+\overrightarrow{G'A'}+\overrightarrow{BG}+\overrightarrow{GG'}+\overrightarrow{G'B'}+\overrightarrow{CG}+\overrightarrow{GG'}+\overrightarrow{G'C'}\right)\)
\(=\dfrac{1}{3}.3.\overrightarrow{GG'}=\overrightarrow{GG'}\)